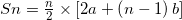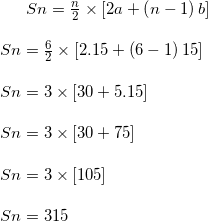Berapakah Jumlah Bilangan Kelipatan 3 Yang Habis Dibagi 5 Antara 10 dan 100?

Untuk soal yang seperti, ada triknya tersendiri.

Dan jangan khawatir, alasannya adalah disini akan dibahas bagaimana cara memecahkan soal tipe ini diikuti langkah-langkahnya.

Contoh soal :

1. Berapakah jumlah bilangan kelipatan 3 yang habis dibagi 5 antara 10 dan 100?

Mari kita amati langkah-langkahnya..

Langkah 1 ⇒ evaluasi soal

Trik pertama

Bilangan kelipatan 3 merupakan deret yang memiliki beda (b) = 3. Nah, kita perlu menentukan sedikit deret kelipatan 3 ini sehabis angka 10.

Kelipatan 3 yang dimulai sehabis 10 ialah 12, jadi deretnya seperti ini.

12, 15, 18, 21, 24, 27, 30,…… 99.

Deret yang terakhir adalah 99, alasannya adalah dihentikan lewat dari 100 (ingat antara 10 dan 100).

Trik kedua

Mari perhatikan lagi deretnya..

12, 15, 18, 21, 24, 27, 30,…… 99

Dari deret diatas, yang habis dibagi 5 ialah mulai dari 15 sesudah itu 30, dan seterusnya.
Kaprikornus deretnya 15, 30, 45, 60…..90.

Sekarang kita sudah ketemu dengan deret kelipatan 3 yang habis dibagi oleh 5 dan mampu ditulis lengkap mirip ini.

15, 30, 45, 60, 75, 90

Langkah 2 ⇒ mencari jumlahnya

Nah, deret kelipatan 3 yang habis dibagi 5 antara 10 dan 100 mempunyai beda (b) = 15 dan deret lengkapnya mirip ini.

15, 30, 45, 60, 75, 90

Untuk mencari jumlahnya, tinggal ditambahkan saja satu per satu.

Jumlah = 15 + 30 + 45 + 60 + 75 + 90

Jumlah = 315.

Atau bisa juga dengan menggunakan rumus jumlah (Sn).

Ingat kembali deretnya..
15, 30, 45, 60, 75, 90

Rumusnya yakni :

Masukkan nilai a, b dan n ke dalam rumus tersebut..

Nah, alhasil sama dengan dijumlahkan biasa..

Antara 24 dan 40 disisipkan 3 bilangan sehingga menjadi deret aritmetika, berapakah ketiga bilangant tersebut?

Jumlah 3 bilangan ganjil berurutan adalah 45. Berapakah ketiga bilangan tersebut?