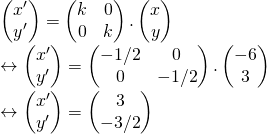Refleksi
Soal dan Pembahasan ❶
Tentukanla bayangan titik P(-6,3) oleh dilatasi kepada titik sentra O(0,0) dengan faktor skala -1/2 .
Pembahasan:
Dengan demikian, x’ = 3 dan y’ = -3/2.
Jadi, bayangan titik P(-6,3) oleh dilatasi kepada titik pusat O(0,0) dengan faktor skala -1/2 adalah P'(3 , -3/2).
2. Dilatasi Terhadap Titik Pusat A(a,b)
Jika titik P(x,y) didilatasikan kepada titik sentra A(a,b) dengan faktor skala k, maka bayangannya ialah P'(x’,y’) dengan
x’ – a = k(x – a) dan y’ – b = k(y – b)
Dengan persamaan matriks, korelasi di atas dapat ditulis:
$\begin pmatrix x’\\y’\end pmatrix =\begin pmatrix k&0\\0&k\end pmatrix .\begin pmatrix x-a\\y-b\end pmatrix +\begin pmatrix a\\b\end pmatrix $
Baca Juga: Soal dan Pembahasan Rotasi (Perputaran)
Soal dan Pembahasan ❷
Tentukanlah bayangan titik P(2,-1) oleh dilatasi kepada titik sentra A(3,4) dengan aspek skala -3.
Pembahasan:
$\begin pmatrix x’\\y’\end pmatrix =\begin pmatrix k&0\\0&k\end pmatrix .\begin pmatrix x-a\\y-b\end pmatrix +\begin pmatrix a\\b\end pmatrix $
⟺ $\begin pmatrix x’\\y’\end pmatrix =\begin pmatrix -3&0\\0&-3\end pmatrix .\begin pmatrix 2-3\\-1-4\end pmatrix +\begin pmatrix 3\\4\end pmatrix $
⟺ $\begin pmatrix x’\\y’\end pmatrix =\begin pmatrix -3&0\\0&-3\end pmatrix .\begin pmatrix -1\\-5
\end pmatrix +\begin pmatrix 3\\4\end pmatrix $
\end pmatrix +\begin pmatrix 3\\4\end pmatrix $
⟺ $\begin pmatrix x’\\y’\end pmatrix =\begin pmatrix 3\\15\end pmatrix +\begin pmatrix 3\\4\end pmatrix $
⟺ $\begin pmatrix x’\\y’\end pmatrix =\begin pmatrix 6\\19\end pmatrix $
Dengan demikian x’ = 6 dan y’ = 19.
Jadi, bayangan titik P(2,-1) oleh dilatasi kepada titik sentra A(3,4) adalah P'(6,19).
Demikian postingan “Soal dan Pembahasan Dilatasi (Perkalian) dengan Matriks” ini, gampang-mudahan mampu membuat lebih mudah anda menyelesaikan soal-soal yang berhubungan dengan dilatasi (perkalian).