Dalam kesempatan ini akan dilanjutkan materi tentang acara linear.
Dalam kesempatan ini akan dibahas sampai tuntas ihwal permasalahan-permassalahan program linear.
Adapun yg akan dibahas di sini antara lain perihal menentukan nilai optimum (maksimum & minimum) daerah solusi dr tata cara pertidaksamaan linear dua variabel, Memodelkan metode pertiddaksamaan linear dua variabel dr permasalahan sehari-hari, & menentukan penyelesaiaannya.
A. Menentukan Nilai Optimum Fungsi Objektif dr Daerah Penyelesaian SPtLDV
Dalam menentukan nilai optimum dr fungsi objektif, lazimnya beberapa hal yg dikenali dalan soal ialah berupa grafik solusi atau bentuk/model sistem pertidaksamaan linear dua variabelnya. Kita disuruh menentukan nilai optimum dr fungsi objektif yg diketahui.
Perhatikan pola berikut.
Contoh 1.
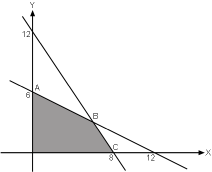
Perhatikan grafik & tempat solusi dr SPLDV berikut.
Tentuan nilai maksimum Z = 2x + 5y dr kawasan penyelesaian (tempat yg diarsir) pada gambar di atas.
Jawaban:
Berdasarkan gambar di atas diperoleh metode pertidaksamaan berikut.
3x + 2y ≤ 24 . . . (1)
x + 2y ≤ 12 . . . (2)
x ≥ 0, y ≥ 0
Menentukan koordinat titik B (titik potong kedua grafik).
3x + 2y = 24
x + 2y = 12
———– –
2x = 12
x = 6
Substitusikan x = 6 ke dlm persamaan (2).
x + 2y = 12 maka 6 + 2y = 12
2y = 6
y = 3
Kaprikornus, koordinat titik B(6, 3).
Uji titik pojok
|
Titik Pojok
|
f(x, y) = 2x + 5y
|
|
A(0, 6)
B(6, 3)
C(8, 0)
|
2 · 0 + 5 · 6 = 30
2 · 6 + 5 · 3 = 27
2 · 8 + 5 · 0 = 16
|
Kaprikornus, nilai maksimumnya yaitu 30.
Contoh 2.
Trik dan Cara Cepat Menghitung / Menentukan Limit Fungsi Tak Hingga
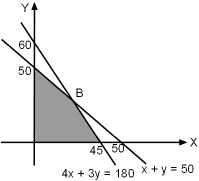
Tentukan nilai maksimum dr fungsi objektif F = 3x + 4y dr tempat yg memenuhi metode pertidaksamaan 4x + 3y ≤ 36 & x + y ≤ 10, x ≥ 0, y ≥ 0.
Jawaban:
Daerah yg menyanggupi metode pertidaksamaan 4x + 3y ≤ 36 & x + y ≤ 10, x ≥ 0, y ≥ 0 dapat digambarkan sepertidi bawah ini.
Selanjutnya, menentukan koordinat titik potong kedua garis pada grafik.
Misalkan titik potong kedua garis yakni titik B.
Dengan cara eliminasi y dr kedua persamaan garis diperoleh pembuatan berikut.
4x + 3y = 36
3x + 3y = 30 __
————–
x = 6
Substitusikan x = 6 ke persamaan x + y = 10, sehingga 6 + y = 10, diperoleh y = 4.
Makara, koordinat titik B(6, 4).
Untuk menentukan nillai maksimum dr fungsi objektif, kita gunakan Uji titik pojok kepada fungsi objektif f(x, y) = 3x + 4y
|
Titik Pojok
|
F(x, y) = 3x + 4y
|
|
A(10, 0)
B(6, 4)
C(0, 9)
|
3 ·10 + 4 · 0 = 30
3 · 6 + 4 · 4 = 34
3 · 0 + 4 · 9 = 36 (maksimum)
|
Jadi, nilai maksimumnya yakni 36.
B. Menentukan atau Membuat Model Sistem Pertidaksamaan Linear Dua Variabel (SPLDV) dr Permasalahan Sehari-hari (Kontekstual)
Berikut ini akan kami berikan cara membuat versi matematika (dalam bentuk SPLDV) dr permasalahan sehari-hari. Dalam hal ini yg menjadi kunci dlm pemodelan adalah pemisalan variabel-variabel dlm bentuk x & y, kata-kata ketidaksamaan seperti ” paling banyak”, “tidak lebih”, “sedikitnya” atau paling sedikit. Kata-kata tersebut mampu disimbolkan dgn tanda ketidaksamaan.
Untuk lebih jelasnya, perhatikan pola berikut,
Contoh 3
Seorang pebisnis kue akan memproduksi kue donat dgn ongkos Rp1.250,00 per buah & kudapan manis brownies dgn harga Rp1.500,00 per buah. Pengusaha roti tersebut mempunyai modal Rp1.500.000,00 & bisa memproduksi 1.150 kudapan manis setiap harinya. Jika x menyatakan banyak kudapan manis donat & y menyatakan banyak kue brownis, pastikan model matematika yg tepat dr permasalahan di atas.
Jawaban:
Misalkan x = banyak kudapan manis
y = banyak kudapan manis brownis
Menentukan versi matematika
(i) Dilihat dari modal & ongkos buatan (optimal Rp1.500.000,-)
1.250x + 1.500y ≤ 1.500.000
5x + 6y ≤ 6.000
(ii) Dilihat dr kemampuan buatan (banyak roti), minimal 1.250 roti
x + y ≥ 1.150
(iii) x ≥ 0
(iv) y ≥ 0
Makara, versi metode pertidaksamaannya adalah 5x + 6y
≤ 6.000, x + y ≥ 1.150,
x ≥ 0,
y ≥ 0.
Contoh 4
Sebuah rumah sakit membutuhkan paling sedikit 15.000 unit kalori & 12.000 unit protein setiap harinya. Setiap 1 kg daging sapi mengandung 500 unit kalori & 300 unit protein. Sedangkan setiap 1 kg ikan segar mengandung 500 unit kalori & 400 unit protein. Jika x menyatakan banyaknya daging sapi (dalam kg) & y menyatakan banyaknya ikan segar (dalam kg), Tentukan versi permasalahan di atas.
Jawaban:
Misalkan: x = banyak daging sapi (dalam kg)
y = banyak ikan segar (dalam kg)
|
|
Unit Kalori
|
Unit Protein
|
|
Daging sapi (x)
Ikan segar (y)
|
500x
300y
|
300x
400y
|
|
|
15.000
|
12.000
|
Model metode pertidaksamaan linear
(i) Dilihat dr unit kalori yg dibituhkan
500x + 300y ≥ 15.000
5x + 3y ≥ 150
(ii) Dilihat dr unit protein yg dibuthkan
300x + 400y ≥ 12.000
3x + 4y ≥ 120
(iii) x ≥ 0
(iv) y ≥ 0
Makara, versi tata cara pertidaksamaannya yaitu 5x + 3y ≥ 150, 3x + 4y ≥ 120, x ≥ 0, y ≥ 0.
C. Menyelesaikan Permasalahan Sehari-hari (Kontekstual) Menggunakan Konsep Program Linear
Pada Bagian terakhir pada materi program linear kali ini ialah menuntaskan permasalahan yg berkaitan dgn acara linear. Penyelesaian masalah keseharian ini merupakan adonan dr beberapa bahan yg sudah diterangkan dr awal.
Langkah-langkah menyelesaikan permasalahan acara linear (memilih nilai optimum) yg berkaitan keseharian.
1. Tentukan model matematika
2. Buat dlm bentuk grafik untuk menyaksikan daerah penyelesaian
3. Tentukan titik-titik pojok kawasan penyelesaian
4. Tentukan nilai pojok-pojok tersebut
5. Tentukan nilai optimumnya (maksimum / minimum)
Lebih jelasnya perhatikan teladan permasalahan berikut.
Contoh 5
Pak Dahlan akan menambah barang jualan helmnya. Dengan keterbatasan tempat, helm jenis A & jenis B tak melampaui 50 helm. Harga pembelian helm jenis A Rp120.000,00 & harga helm jenis B Rp90.000,00. Dari penjualan helm-helm tersebut diperoleh keuntungan Rp30.000,00 untuk setiap helm jenis A & Rp25.000,00 untuk setiap helm jenis B. Jika versi pedagang tersebut Rp5.400.000,00, Tentukan keuntungan maksimum yg diperoleh pedagang tersebut. Cara Mudah dan Cara Benar dalam Menentukan dan Menghitung Median pada Tabel Distribusi Frekuensi dan Histogram
Jawaban:
Misalkan: x = banyak helm jenis A
y = banyak helm jenis B
Model sistem pertidaksamaan
x + y ≤ 50 . . . (1)
120.000x + 90.000y ≤ 5.400.000
4x + 3y ≤ 180 . . . (2)
x ≥ 0
y ≥ 0
Fungsi objektif f(x, y) = 30.000x + 25.000y
Grafik tata cara pertidaksamaan
Menentukan titik potong B.
x + y = 50 × 4 4x + 4y = 200
4x + 3y = 180 × 1 4x + 3y = 180
———————- –
y = 20
Substitusikan y = 20 ke dlm persamaan (1)
x + 20 = 50 atau x = 50 – 20
x = 30
Diperoleh titik B(30, 20)
Uji titik pojok
|
|
f(x, y) = 30.000x + 25.000y
|
|
(0, 50)
(30, 20)
(45, 0)
|
30.000 × 0 + 25.000 × 50 = 1.250.000
30.000 × 30 + 25.000 × 20 = 1.400.000
30.000 × 45 + 25.000 × 0 = 1.350.000
|
Kaprikornus, keuntungan maksimum yg dapat diperoleh Pak Dahlan sebesar Rp1.400.000,00.