Modus Adalah : Nilai, Rumus, Contoh Soal dan Penyelesaiannya – Apakah yang dimaksud dengan modus dalam ilmu matematika ? Pada kesempatan ini Seputarpengetahuan.co.id akan membahasnya, mencakup pemahaman,rumus dan tentunya hal-hal lain yang juga melingkupinya.Mari kita simak bareng pembahasannya pada postingan di bawah ini untuk lebih dapat memahaminya.
Daftar Isi
Daftar Isi
Modus Adalah : Nilai, Rumus, Contoh Soal dan Penyelesaiannya
Dalam sebuah mata pelajaran matematika, secara sederhana definisi dari modus yakni nilai yang paling sering muncul. Dalam data kelompok yang telah dihidangkan frekuensinya, modus suatu nilai yang mempunyai frekuensi terbesar.
Modis trebagi atas dua bentuk yaitu ,yakni modus data tunggal dan modus data golongan. Pada ketika anda ingin mencari nilai dari modus yang terdapat pada data tunggal mampu di bilang cukup gampang untuk data kebanyakan, tetapi sedangkan jika anda mencari sebuah nilai pada modus data kalangan mampu dikatakan tidak begitu mudah mirip pada saat pencarian data pada modus data tunggal, oleh sebab itu kita perlu menggunakan sebuah rumus tertentu untuk menemukannya.
Dalam bahan modus kebanyakan memiliki nilai lebih dari 1. Apabila anda telah mendapatkan nilai dengan frekuensi paling besar ini trdapat 2 nilai, maka modusnya yakni kedua nilai tersebut. Begitu juga jikalau 3, 4, dan seterusnya. Namun, yang bisanya nilai modus disebutkan hanya 1.
Lambang modus dalam persamaan yaitu Mo.
Modus Data Tunggal
Data tunggal adlah suatu data mentah yang masih acak. Pada umumnya data ini telah mampu eksklusif dipakai kalau cuma memperlihatkan jumlah data optimal 30 buah.
Data tunggal ini dalam tingkat lanjutan akan diolah dalam bentuk tabel dan dalam bentuk diagram statistika semoga memudahkan membacanya.
Modus dari data tunggal bisa dilihat dengan meneliti nilai manakah yang paling sering timbul.
-
Cara Menentukan Nilai Modus Pada Data Tunggal
Contoh Soal
Perhatikan dua acuan soal di berikut ini agar anda mampu paham dengan nilai modus ialah semenjak tahapan dasar.
a. hitunglah modus dari tinggi badan pada siswa kelas 11 ialah: 142 145 143 148 144 142 146 148 147 146 145
Jawab:
Dalam data di atas menybutkan bahwa nilai 142 muncul sebanyak 2 kali, 143 = 1, 144 = 1, 145 = 2, 146 = 2, 147 = 1, dan 148 = 2
Modus dari data di atas adalah 142, 14, 146, dan 148.
b. Tentukan nilai modus dari data nilai matematika dari siswa kelas 9 ialah: 10, 9, 8, 7, 8, 9, 8, 6, 6, 7, 9, 8, 7, 9, 10, 9, 8, 7, 7, 6, 7, 8, 9, 10, 9, 8, 6, 7, 9, 10
Untuk data yang lebih dari 10 akan lebih mudah untuk diurutkan apalagi dulu. Dengan demikian anda akan mampu menentukan nilai median sekaligus nilai modusnya. Walaupun seperti itu, anda hanya perlu menjumlah modus dulu kali ini.
Data diurutkan menjadi:
6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10
Dari data yang telah diurutkan kita mampu lihat bahwa nialai yang sering timbul yakni angka = 9. Artinya, berdasarkan dari nilai yang ada, bahwa siswa kelas VI dengan nilai 9 lah yang paling banyak didapatkan.
Modus Data Kelompok
Dalam modus data golongan di sini masih gampang untuk anda pahami. Data kelompok masih dalam data kelompok yang sederhana.
-
Rumus Modus Data Kelompok
Pada data berkelompok, modus mampu diputuskan dengan
Mo = tb + (d1 / (d1 + d2)) k
Keterangan:
- Mo : modus data kelompok
- tb: tepi bawah kelas modus
- d1 : frekuensi kelas modus dikurangi dengan frekuensi kelas yang sebelumnya
- d2 : frekuensi kelas modus dikurangi dengan frekuensi yang kelas sesudahnya
- k : panjang kelas
Contoh Soal
1. Gambar lah data golongan dibawah ini dalam bentuk tabel dan tentukan juga nilai modusnya!
6, 9, 10, 8, 8, 9, 8, 6, 6, 7, 9, 8, 7, 9, 8, 9, 8, 7, 7, 10, 7, 8, 9, 10, 9, 7, 6, 7, 9, 10
Jawab:
Data sesudah diurutkan:
6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10
Masukkan data tersebut dalam bentuk tabel dengan cara memperhitungkan frekuensi banyaknya siswa yang memperoleh nilai tertentu.
| Nilai Ulangan Matematika | Jumlah siswa (frekuensi) |
| 6 | 4 |
| 7 | 7 |
| 8 | 7 |
| 9 | 8 |
| 10 | 4 |
| Total | 30 |
Modus data golongan dalam tabel yaitu 9 alasannya adalah mendapatkan frekuensi dengan nilai paling besar.
2. Tentukan lah modus dari data yang ada di bawah ini!
Tabel Berat Badan Siswa
| Berat Badan (kg) | Jumlah Siswa (frekuensi) |
| 35 | 8 |
| 36 | 9 |
| 37 | 8 |
| 38 | 7 |
| 39 | 7 |
| 40 | 6 |
| Total | 45 |
Jawab:
Nialai modus dari data yang ada di atas yakni berat badan 36 kg alasannya berat badan dari 36 ini memiliki nilai frekuensi terbesar.
Modus dari data Kelompok dengan Tabel Distribusi Frekuensi
Tabel distribusi frekuensi juga yaitu termasuk dalam data kalangan. Hanya saja, pada tabel tersebut nilai data dituliskan dalam bentuk range tertentu yang disebut dengan interval atau kelas.
Meskipun demikian, nilai modus untuk data kalangan tersebut dirumuskan:
Keterangan :
Mp = modus
• Xi = tepi bawah kelas modus
• fi = frekuensi kelas modus
• f1 = selisih antara frekuensi kelas modus ialah dengan kelas sebelumnya
• f2 = selisih antara freuensi kelas modus ialah dengan kelas sesudahnya
Contoh Soal
Mari anda hitung nilai modus dari data tabel yang ada dibawah ini!
| Nilai | Frekuensi |
| 11 – 20 | 3 |
| 21 – 30 | 5 |
| 31 – 40 | 10 |
| 41 – 50 | 11 |
| 51 – 60 | 8 |
Jawab:
Frekuensi dari nilai terbesar ialah 11 berada pada kelas 41-50, sehingga 41 – 50 disebut bahwa kelas modus dan diperoleh:
- Xi = tepi bawah kelas modus yaitu = 41- 0,5 = 40,5
- fi = kelas modus = 11
- f1 = selisih antara kelas modus dengan kelas sebelumnya yaitu = 11 – 10 = 1
- f2 = niali selisih dari kelas modus dengan kelas setelahnya adalah = 11 – 8 = 3
- p = panjang kelas = tepi atas kelas – tepi bawwah kelas = 50,5 – 40,5 = 10
modusnya yakni = 40,5 + (11/(1+3))10 = 40,5 + 27,5 = 68

Contoh Soal
Amati tabel berikut ini dan cari modus kelompoknya.
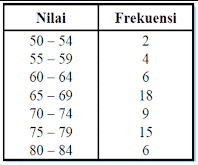
Jawaban:
Frekwensi dari modus pada data diatas yaitu 18, sedangkan pada kelas modus diatas adalah 65-69, sementara tepi bawah dari frekwensi modus (b) = 64,5.
d1= 18 – 6 = 2
d2= 18 – 9 = 9
l= 69,5 – 64,5 = 5
Mo= b0 + (d1/d1+d2) x l = 64,5 + (12/12+9) x 5 = 64,5 + 12/21 x 5 = 64,5 + 2,86 = 67,36.
Demikianlah ulasan dari Seputarpengetahuan.co.id wacana Modus Adalah : Nilai, Rumus, Contoh Soal dan Penyelesaiannya, supaya mampu menambah pengetahuan dan wawasan kalian. Terimakasih sudah berkunjung dan jangan lupa untuk membaca artikel yang lain.