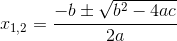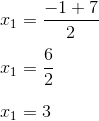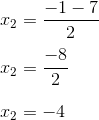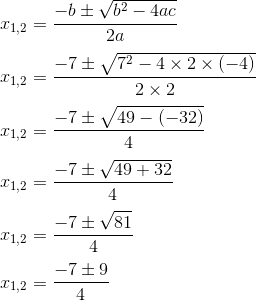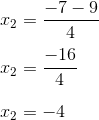Salah satu cara untuk mendapatkan penyelesaian dari suatu fungsi kuadrat yakni menggunakan rumus ABC.
Kita akan secepatnya mencobanya..
1. Carilah penyelesaian x² + x – 12 = 0 dengan menggunakan rumus ABC!!
Mari kita lihat ciri dari persamaan kuadrat..
Persamaan kuadrat mampu dibentuk seperti ini.
ax² + bx + c = 0
- a = angka di depan x²
- b = angka di depan x
- c = ialah angka yang tidak mengandung variabel.
x² + x – 12 = 0
- a = 1 (alasannya adalah tidak ada angka di depan x², maka angkanya sama dengan 1)
- b = 1 (alasannya adalah tidak ada angka di depan x, maka angkanya sama dengan 1)
- c = -12 (tanda miuus juga ikut ditulis ya)
Mencari x₁
Untuk mendapatkan x₁, kita akan menggunakan tanda (+) dulu.. Yang pecahan plus minus-nya kita gunakan (+).
Mencari x₂
Selanjutnya kita gunakan tanda (-)
Nah, kedua nilai x sudah diperoleh, yakni :
- x₁ = 3
- x₂ = -4.
2. Carilah penyelesaian 2x² + 7x – 4 = 0 dengan memakai rumus ABC!!
ax² + bx + c = 0
- a = angka di depan x²
- b = angka di depan x
- c = adalah angka yang tidak mengandung variabel.
- a = 2
- b = 7
- c = -4 (tanda minus juga ikut ditulis)
Mencari x₁
Untuk menerima x₁, kerjakan yang penjumlahan lebih dahulu..
Mencari x₂
Sekarang dikurangkan..
Nah, kedua nilai x sudah diperoleh, yakni :
- x₁ = ½
- x₂ = -4.