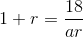Jumlah Suku ke-2 dan ke-3 Deret Geometri 18, Jumlah Suku ke-3 dan ke-4 = 36. Berapakah Suku ke 5?

Masing-masing suku diganti dengan rumusnya sendiri-sendiri, sehingga kita mampu menerima persamaan.

Persamaan yang mampu kita pakai untuk mencari suku awal dan rasio.

Berikut ialah teladan soalnya :

Soal :

1. Jumlah suku ke-2 dan ke-3 sebuah deret geometri ialah 18. Sedangkan jumlah suku ke-3 dan ke-4 yakni 36.

Berapakah suku ke-lima?

Kita lihat penjumlahan yang pertama.

Jumlah suku ke-2 dan ke-3 = 18

Rumus suku deret geometri yakni :

Un = a.r^n-1

Kemudian kita bisa mencari suku ke-2.

U₂ = a.r^2-1

U₂ = a.r¹

U₂ = a.r ….①

Un = a.r^n-1

U₃ = a.r^3-1

U₃ = a.r² ….②

Kemudian :

U₂ + U₃ = 18

ganti U₂ sesuai persamaan ①
ganti U₃ sesuai persamaan ②

ar + a.r² = 18

untuk ruas kiri difaktorkan, sehingga bisa dikeluarkan “ar”

ar (1 + r) = 18

pindahkan ar ke ruas kiri menjadi pembagi

….③

Jumlah suku ke-3 dan ke-4 = 36

Un = a.r^n-1

U₃ = a.r^3-1

U₃ = a.r² ….④

Un = a.r^n-1

U₄ = a.r^4-1

U₄ = a.r³ ….⑤

U₃ + U₄ = 36

ganti U₃ dengan hasil pada persamaan ④
ganti U₄ dengan hasil pada persamaan ⑤

ar² + ar³ = 36

faktorkan yang diruas kiri dengan mengeluarkan ar²

ar²(1 + r) = 36 …⑥

Mencari nilai “a” dan “r”

Sekarang kita akan menggunakan persamaan ③ dan ⑥

ar²(1 + r) = 36 …⑥

Masukkan persamaan ③ dan ganti 1+r

Cara :

“a” dicoret dengan “a” dan hilang
r² dibagi r, sisa r

r = 2.

Setelah mendapatkan “r”, kita mampu mencari “a” memakai persamaan ⑥

ar²(1 + r) = 36

ganti r = 2

a.2²(1 + 2) = 36

Diketahui U3 dan U6 Dari Deret Geometri Adalah 12 dan 96. Berapakah U2?

4a (3) = 36

12a = 36

Untuk menerima a, bagi 36 dengan 12

a = 36 : 12

a = 3.

Mencari suku ke-5

Rumus mencari suku pada deret geometri yakni :

Un = a.r^n-1

Dan kita bisa mencari suku ke-5

U₅ = a.r^5-1

U₅ = a.r⁴

ganti a = 3
ganti r = 2

U₅ = 3.2⁴

U₅ = 3.16

U₅ = 48

Jadi diperoleh U₅ = 48

Baca juga ya :