Faktor, Kelipatan, Faktor Prima, Faktorisasi Prima, KPK dan FPB (2)

by

Dalam kesempatan ini kita akan membahas & mencar ilmu ihwal Faktor prima, faktorisasi prima, Kelipatan persekutuan terkecil (KPK) & Faktor komplotan terbesar (FPB) menggunakan faktorisasi prima.

 
Faktorisasi Prima & Faktor Prima


Bilangan prima yaitu bilangan yg sempurna mempunyai dua faktor yaitu 1 & bilangan itu sendiri.
Bilangan prima = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, . . . .

Faktorisasi prima yaitu pembagian terstruktur mengenai suatu bilangan menjadi perkalian-perkalian bilangan prima. Makara, dgn perkalian beberapa bilangan prima diperoleh hasil boilangan itu.
Contoh 
6 = 2 x 3          (2 & 3 ialah bilangan prima)
20 = 2 x 2 x 5  (2 & 5 yaitu bilangan prima)
45 = 3 x 3 x 5  (3 & 5 yaitu bilangan prima)
70 = 2 x 5 x 7  (2, 5, & 7 yaitu bilangan prima)
Bentuk bentuk di atas merupakan acuan faktorisasi prima dr sebuah bilangan.

 Faktor Prima adalah bilangan-bilangan prima yg terdapat pada faktorisasi prima.
Misalkan pada faktorisasi prima di atas.
6 mempunyai aspek prima 2 & 3 .
20 memiliki aspek prima 2 & 5.
45 memiliki faktor prima 3 & 5.
70 memiliki aspek prima 2, 3, & 5.

 Untuk bilangan-bilangan yg kecil, mungkin mudah untuk menciptakan faktorisasi prima. Namun untuk bilangan yg besar perlu aliran yg lebih. Pada potensi ini mari menciptakan faktorisasi bilangan yg lebih besar. Caranya dgn pohon faktor. Prinsip pohon aspek yaitu pembagian bilangan sampai dgn bilangan prima pada ujung-ujungnya.

 Perhatikan cara berikut. 




Faktorisasi prima dr 48
48 = 2 x 2 x 2x 2 x 3 = 24 x 3
Faktor prima = 2 & 3


Faktorisasi prima dr 90
90 = 2 x 3 x 3 x 5 = 2 x 32 x5
Faktor prima = 2, 3 & 5





Faktorisasi prima dr 140
140 = 2 x 2 x 5 x 7 = 22 x 5 x 7
Faktor prima = 2, 5 & 7






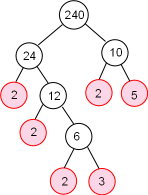
Faktorisasi prima dr 240
240 = 2 x 2 x 2 x 2 x 3 x 5 = 24 x 3 x 5
Faktor prima = 2, 3 & 5






Menentukan  FPB menggunakan Faktorisasi Prima
 
Langkah-langkah memilih FPB
1. Tulislah semua faktorisasi prima dr setiap bilangan
2. Pilihlah bilangan faktor yg sama & kalikanlah
3. Pada bilangan aspek yg ada pangkatnya, seleksilah bilangan dgn pangkat terkecil

 Contoh:
Tentukan FPB dr 60 & 36

 60 = 2 x 2 x 3 x 5 = 22 x 3 x 5
36 = 2 x 2 x 3 x 3 = 22 x 32 
FPB = 22 x 3 = 12 (pada bilangan 3 dipilih pangkat terkecil yaitu 3)

Cara kedua


Bagilah dengan  bilangan prima terkecil/termudah
Pilihlah pembagi yg bisa membagi kedua bilangan

 FPB = 2 x 2 x 3 = 12




Tentukan FPB dr 120 & 300
120 = 2 x 2 x 2 x 3 x 5 = 23 x 3 x 5
300 = 2 x 2 x 3 x 5 x 5 = 22 x 3 x 52 
FPB = 22 x 3 x 5 = 60 (pada bilangan 2 & 5 dipilih pangkat terkecil yaitu 22 dan 5)

 Cara Kedua




Bagilah dengan  bilangan prima terkecil/termudah
Pilihlah pembagi yg bisa membagi kedua bilangan
FPB = 22 x 3 x 5 = 60



Menentukan  KPK memakai Faktorisasi Prima
 
Langkah-langkah memilih FPB
1. Tulislah semua faktorisasi prima dr setiap bilangan
2. Tulislah semua bilangan faktor yg sama
3. Jika ada bilangan faktor yg berpangkat, seleksilah bilangan dgn pangkat paling besar, lalu kalikanlah
Contoh:
Tentukan KPK dr 30 & 48
30 = 2 x 3 x 5
48 = 2 x 2 x 2 x 2 x 3 = 24 x 3

KPK = 24 x 3 x 5 = 240 (pada bilangan 2 dipilih pangkat terbesar yaitu 24 )
Cara kedua

Bagilah dengan  bilangan prima terkecil/termudah
Pilihlah pembagi yg mampu membagi kedua bilangan
Bagilah sampai akhir, kesudahannya 1-1
KPK = 24 x 3 x 5 = 240


Tentukan KPK dr 45, 60, & 75
45 = 3 x 3 x 5 = 32 x 5
60 = 2 x 2 x 3 x 5 = 22 x 3 x 5
75 = 3 x 5 x 5 = 3 x 52 

KPK = 22 x 32 x 52 = 900 (pada bilangan 2, 3, & 5 diseleksi pangkat terbesar)
Cara kedua

KPK = 22 x 32 x 52 = 900





Demikian sedikit klarifikasi wacana faktorisasi prima, faktor prima, KPK & FPB.
Semoga berfaedah.

  Pengantin Wanita Mengaku Gadis Ternyata Janda

Untuk mempelajari permasalahan & solusi dilema keseharian memakai KPK & FPB, teruskan dgn KLIK di bawah ini.

Penyelesaian Permasalahan wacana KPK & FPB