Pelajarancg: 11 MACAM BILANGAN DAN CONTOHNYA. pelajarancg.blogspot.com, – Pengertian: Bilangan prima yakni bilangan bundar dengan tepat dua pembagi integral, 1 dan dirinya sendiri.
Angka 1 bukan bilangan prima, alasannya cuma memiliki satu pembagi.
Kaprikornus bilangan prima terkecil yaitu:
2 , 3 , 5 , 7 ,
Bilangan 4 bukan prima, sebab memiliki tiga pembagi ( 1 , 2 , dan 4 ), dan 6 bukan prima, alasannya adalah memiliki empat pembagi ( 1 , 2 , 3 , dan 6 ).
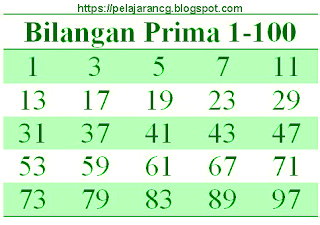 |
| Gambar Bilangan Prima 1 -100 |
Pengertian: Bilangan komposit adalah bilangan bundar yang memiliki lebih dari dua pembagi integral. Singkatnya, Bilangan komposit mempunyai arti bilangan orisinil yang memiliki lebih dari 2 aspek. Suatu bilangan lingkaran nyata dinamakan bilangan komposit bila bilangan itu mempunyai pembagi lain kecuali bilangan itu sendiri dan 1.
Kaprikornus semua bilangan bundar (kecuali 0 dan 1 ) adalah prima atau komposit.
Contoh:
43 ialah prima, sebab satu-satunya pembaginya yaitu 1 dan 43 .
44 yaitu komposit, karena mempunyai 1 , 2 , 4 , 11 , 22 dan 44 sebagai pembagi.
Daftar Isi
Bagaimana cara menentukan bilangan prima?
Pertama-tama, berikut yaitu beberapa cara untuk mengenali apakah suatu bilangan BUKAN prima:
Bilangan apa pun yang lebih besar dari 2 yang ialah kelipatan 2 bukanlah bilangan prima, alasannya mempunyai setidaknya tiga pembagi: 1 , 2 , dan dirinya sendiri. (Ini berarti 2 yaitu satu-satunya bilangan prima yang genap.)
Setiap bilangan yang lebih besar dari 3 yang merupakan kelipatan 3 bukanlah bilangan prima, sebab memiliki 1 , 3 dan dirinya sendiri selaku pembagi. (Contohnya, 303 bukan prima, alasannya adalah 303 3 = 101 .)
Setiap bilangan yang ialah kelipatan 4 juga merupakan kelipatan 2, jadi kita mampu mengesampingkannya.
Setiap bilangan yang lebih besar dari 5 yang merupakan kelipatan 5 bukanlah bilangan prima. (Makara satu-satunya bilangan prima yang diakhiri dengan 0 atau 5 yakni 5 itu sendiri.)
Setiap bilangan yang merupakan kelipatan 6 juga merupakan kelipatan 2 dan 3 , jadi kita dapat mengesampingkannya juga.
Kamu dapat melanjutkan mirip ini… pada dasarnya, Anda hanya perlu menguji pembagian dengan bilangan prima!
Contoh 1:
Apakah 119 prima?
Soal pertama untuk pembagian dengan 2. 119 ganjil, jadi tidak habis dibagi 2 .
Selanjutnya, uji kompetensi keterbagian dengan 3. Tambahkan angka: 1 + 1 + 9 = 11. Karena 11 bukan kelipatan 3, juga 119 . (Ingat teman kurikulum pelajarancg, langkah ini hanya berfungsi untuk menguji pembagian dengan 3 dan 9.)
Karena 119 tidak diakhiri dengan 0 atau a 5 , itu tidak habis dibagi 5 .
Selanjutnya, uji keterbagian dengan 7. Kamu akan menemukan bahwa 119 7 = 17 .
Kaprikornus jawabannya TIDAK… 119 bukan bilangan prima.
Contoh 2:
Apakah 127 prima?
Soal pertama untuk pembagian dengan 2. 127 ganjil, jadi tidak habis dibagi 2 .
Selanjutnya, uji keterbagian dengan 3. Tambahkan angka: 1 + 2 + 7 = 10. Karena 10 bukan kelipatan 3, juga bukan 127 .
Karena 127 tidak diakhiri dengan 0 atau a 5 , itu tidak habis dibagi 5 .
Selanjutnya, uji keterbagian dengan 7. Kamu akan mendapatkan bahwa 7 tidak masuk secara merata.
Bilangan prima berikutnya ialah 11. Tapi 11 juga tidak masuk secara merata.
Kamu mampu berhenti kini … itu mesti prima! Anda tidak butuhterus menilik pembagian dengan bilangan prima berikutnya ( 13 , 17 , 19 , 23 , dll). Alasannya yaitu jika 13 masuk secara merata, maka kita akan memiliki 127 = 13 × n untuk beberapa bilangan n. Tapi kemudian n mesti kurang dari 13 … dan kita sudah tahu bahwa 127 tidak habis dibagi oleh bilangan yang lebih kecil dari 13 .
Jadi jawabannya YA… 127 ialah bilangan prima.
Tentang kurikulum pelajarancg.blogspot.com:
Blog Informasi Berbagai Kurikulum Mata Pelajaran Matematika & Pendidikan Indonesia berbagai tingkatan dari SD/MI, SMP/MTs, Sekolah Menengan Atas/MA/SMK dan Perguruann Tinggi. Istilah kurikulum berasal dari bahasa Latin “curir” yang berarti palri dan “curere” yang mempunyai arti kawasan berpacu. Sehingga kurikulum dapat diartikan sebagai trek atau lajur yang harus dibarengi seseorang untuk mencapai tujuannya. Oleh alasannya adalah untuk mendukung Sekolah melancarkan proses pendidikan di Indonesia maka dibuatlah artikel macam-macam Bilangan dan contoh yang dirangkum pada Blog Kurikulum pelajarancg.blogspot.com