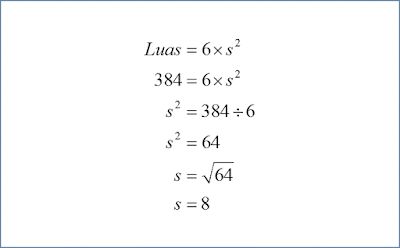Dalam soal kali ini, kita akan melaksanakan pembuktian terbalik dari soal sebelumnya.
Silahkan dibaca dahulu di postingan berikut :
↦ Mencari luas kubus kalau diketahui rusuknya
Soal :
1. Luas permukan suatu kubus ialah 384 cm². Hitunglah panjang rusuknya!
Diketahui :
- Luas permukaan 384 cm²
Dan kini tinggal ikuti rumus luas permukaan dan masukkan nilai yang diketahui.
Langkah-langkahnya :
- Ganti luas dengan 384
- Kemudian bagi 384 dengan 6
Sekarang kita sudah mendapatkan s².
“s” yaitu rusuk kubus-nya.
Untuk mendapatkan s, maka 64 harus diakarkan.
s = 8 cm.
Inilah panjang rusuk kubus yang diminta.
Hasilnya sama dengan soal sebelumnya kan??
Soal :
2. Berapakah panjang rusuk kubus bila luas permukaannya 864 cm²?
Langkah-langkahnya masih sama dengan soal pertama.
Luasnya = 864 cm²
Tulis rumus luas permukaan kubus.
Luas = 6.s²
- ganti luasnya dengan 864
864 = 6.s²
- bagi 864 dengan 6 untuk menerima s²
s² = 864 ÷ 6
s² = 144
- biar mendapatkan “s”, maka 144 mesti diakarkan
s = √144
s = 12 cm.
Makara panjang rusuk kubusnya ialah 12 cm.
Tips
Ketika diketahui luas permukaan, maka rumus luas inilah yang harus dipakai untuk memperoleh rusuk kubus.
Rumusnya sangatlah gampang dihafal mengenang semua rusuk kubus panjangnya sama.
Ingat lagi rumus luas permukaan.
Luas = 6.s²
Langkah yang sempurna yakni membagi luasnya dengan 6 apalagi dulu. Setelah itu kita akan mendapatkan s².
Kemudian akarkan alhasil dan rusuk diperoleh.
Nah…
Semoga membantu ya.
Baca juga ya :