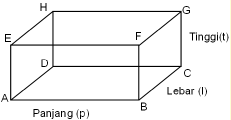
1. Sisi-sisi balok berupa persegi panjang. Perhatikan sisi ABCD, EFGH, ABFE, CDHG, ADHE, & BCGF. Sisi-sisi tersebut mempunyai bentuk persegi panjang. Dalam balok, minimal mempunyai dua pasang sisi yg berupa persegi panjang.
2. Rusuk-rusuk yg sejajar mempunyai ukuran sama panjang. Perhatikan rusuk-rusuk balok pada gambar diatas. Kelompok rusuk-rusuk yg sejajar sebagai berikut.
rusuk AB, CD, EF, & GH,
rusuk AE, BF, CG, & DH,
rusuk AD, BC, FG, & EH.
3. Setiap diagonal bidang pada sisi yg berhadapan memiliki ukuran sama panjang. Dari gambar terlihat bahwa panjang diagonal bidang pada sisi yg berhadapan, yakni ABCD dgn EFGH (AC = BD = EG = FH), ABFE dgn DCGH (AF = BE = CH = DG), & BCFG dgn ADHE (AH = ED = BG = CF).
4. Setiap diagonal ruang pada balok mempunyai ukuran sama panjang. Diagonal ruang pada balok ABCD.EFGH, yakni AG, EC, DF, & HB memiliki panjang yg sama.
5. Setiap bidang diagonal pada balok memiliki bentuk persegi panjang. Perhatikan balok ABCD.EFGH pada gambar dibawah ini. Bidang diagonal balok BDHF memiliki bentuk persegi panjang. Begitu pula dgn bidang diagonal yang lain. Pasangan-passangan bidang diagonal yg sama bentuk & ukuran.
Bidang ACGE = BDHF
Bidang ABGH = CDEF
Bidang ADFG = BCHE
Contoh Soal:
1. Tentukan Luas permukaan & Volume balok yg berukuran panjang 7 cm, lebar 5 cm & tinggi 4 cm.
Jawaban:
Luas Permukaan = L = 2 x (p x l + p x t + l x t)
= 2 x (7 x 5 + 7 x 4 + 5 x 4)
= 2 x (35 + 28 + 20)
= 2 x 83
= 168
Makara luas permukaan balok yakni 168 cm2.
Volume Balok = V = p x l x t
= 7 x 5 x 4
= 140
Jadi, volume balok yaitu 140 cm3.
2. Diketahui balok dgn volume 675 cm2. Jika tinggi perbandingan panjang & lebar 5 : 3 & tinggi balok 5 cm, pastikan :
a. Ukuran panjang & lebar
b. Luas permukaan balok.
Jawaban:
Misalkan panjang balok = 5n & lebar balok = 3n
Volume Balok = V = p x l x t
675 = 5n x 3n x 5
675 = 75 n2.
n = 3
= 2 x (15 x 9 + 15 x 5 + 9 x 5)
= 2 x (135 + 75 + 45)
= 2 x 255
= 510
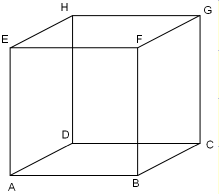
2. Kubus
Contoh Soal
1. Tentukan volume & luas permukaan kubus yg mempunyai panjang rusuk 8 cm.
Jawaban:
Volume = s x s x s
= 8 x 8 x 8
= 512
Makara, volume kubus ialah 512 cm3.
Luas Permukaan = 6 x s x s
= 6 x 8 x 8
= 384
Jadi, luas permukaan kubus yaitu 384 cm2.
2. Diketahui kubus dgn volume 1.728 cm3. Tentukan luas permukaan kubus tersebut.
Jawaban:
Volume = s x s x s
1.728 = s3
s = 12 cm
Luas Permukaan = 6 x s x s
= 6 x 12 x 12
= 864
Makara, luas permukaan kubus yakni 864 cm2
3. Sebuah kubus mempunyai panjang rusuk 6 cm. tentukan:
a. panjang diagonal sisi
b. panjang diagonal ruang
c. Luas bidang diagonal
Jawaban:
a. Panjang diagonal sisi = sV2 (V adalah tanda akar)
= 6 V2 cm
b. Panjang diagonal ruang = sV3
= 6V3 cm
c. Luas Bidang diagonal = sisi x panjang diagonal sisi
= 6 x 6V2
= 36V2 cm2
Itulah beberapa klarifikasi ihwal Balok & Kubus.
Selamat berguru.