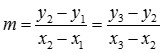Jika sebuah titik terletak pada satu garis lurus, berarti ketiga titik itu berada dalam satu gradien yang serupa. Nah, inilah dasar yang hendak dipakai untuk menjawab soal dalam bentuk mirip ini. Ayo kita lihat lagi soalnya..
Soal
1. Tiga buah titik (1,3), (-2, -3) dan (a,9) terletak pada satu garis lurus. Berapakah nilai dari “a”?
Diatas telah dijelaskan kalau tiga titik yang berada pada satu garis lurus akan memiliki gradien yang sama. Masih ingat cara mencari gradien dari dua titik?
Untuk mendapatkan gradien, maka kita memerlukan sekurang-kurangnyadua titik. Nah mari kita lihat lagi caranya..
Titik pertama , (1,3) :
- x₁ = 1
- y₁ = 3
Titik kedua, (-2, -3) :
- x₂ = -2
- y₂ = -3
Titik ketiga, (a, 9) :
- x₃ = a
- y₃ = 9
Rumus untuk gradien dari dua titik dan yang mau digunakan dalam soal ini yaitu :
Kita masukkan eksklusif masing-masing x dan y ke persamaan diatas, sehingga mampu diperoleh nilai “a”-nya berapa.
- masukkan masing-masing nilai x dan y
- -6 dibagi dengan -3 hasilnya yaitu 2 dan disampingnya yaitu 12 dibagi a + 2
Sekarang kita kalikan silang.
- 2 dikali dengan (a+2) sedangkan 12 tetap tidak berganti.
2 × (a + 2) = 12
- untuk membuka kurung (a+2), kalikan 2 dengan a dan kalikan 2 dengan 2.
- jadi angka 2 yang ada diluar kurung dikalikan dengan semua angka di dalam kurung.
2a + 4 = 12
- pindahkan +4 ke ruas kanan sehingga menjadi -4
2a = 12 – 4
2a = 8
- Untuk mendapatkan a, maka 8 mesti dibagi dengan 2
a = 8 : 2
a = 4.
Nah, telah diperoleh nilai dari “a” ialah 4.
Bagaimana bila gradien yang dipakai titik kedua di kurang titik pertama dan titik ketiga di kurang titik pertama juga?
Hasilnya sama kok!!
Makara jangan ragu untuk menjajal menggunakan rumus yang ini.
Gradien itu adalah penghematan dua titik, entah itu titiknya berdekatan atau berjauhan. Mari kita coba untuk perkara yang ini..
Titik-titik yang digunakan masih sama dengan soal diatas ya..
Sekarang kita kalikan silang antara 2 dan (a-1), sedangkan 6 tetap tidak berganti.
2 × (a – 1) = 6
- yang didalam kurung dikalikan dengan 2 semua, sehingga kurungnya terbuka
2 × a – 2× 1 = 6
2a – 2 = 6
- pindahkan -2 ke kanan dan menjadi +2
2a = 6 + 2
2a = 8
Untuk mendapatkan a, bagi delapan dengan dua
a = 8 : 2
a = 4.
Hasilnya sama bukan?
Selamat mencoba ya..
Baca juga :