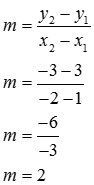Untuk menerima hasil dari soal mirip ini, kita bisa mencari persamaan garisnya apalagi dahulu. Caranya yaitu dengan menggunakan dua buah titik yang telah dikenali.
Tapi jikalau malas mencari persamaan garisnya, tidak persoalan kok..
Ada satu cara lagi yang jauh lebih singkat dibandingkan harus mencari persamaan garisnya. Kaprikornus tidak perlu membuang waktu berlebihan.
Ok, mari lihat lagi soalnya..
1. Diketahui tiga buah titik (1,3), (-2, -3) dan (a,5) berada dalam satu garis lurus. Berapakah nilai dari a?
Mari kita perhatikan klarifikasi dibawah ini!!
Analisa soal
Nah, sudah diterangkan dalam soal dengan terang benderang bahwa ketiga titik ini berada dalam satu garis lurus.
Jika ada buku kotak-kotak, maka tinggal pastikan saja titik-titiknya dan tariklah garis lurus.
Panjangkan garisnya hingga mencapai nilai “sumbu y” sama dengan 5. Kemudian lihatlah berapa nilai x-nya.
Itu kalau ada buku kotak-kotak, kalau tidak ada kita mampu menghitungnya.
Caranya?
Ciri-ciri beberapa titik yang berada dalam satu garis adalah mempunyai gradien yang serupa.
Nah, gradien inilah yang akan menjadi referensi kita dalam memecahkan soal berikut ini..
Mencari jawaban
Masih ingat rumus gradien?
Gradien (m) dirumuskan selaku berikut..
Trus caranya bagaimana?
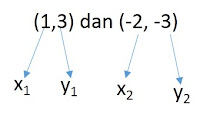
Kita cari gradiennya dari dua buah titik yang sudah dikenali dulu, yakni (1,3) dan (-2, -3)
Tentukan dahulu mana yang menjadi x1, y1, x2 dan y2. Sekarang kita masukkan ke rumus untuk mencari gradiennya.
Nah, gradien sudah ketemu. Sekarang kita mampu terapkan cara yang serupa untuk mendapatkan nilai “a”.
Titik yang dipakai yaitu (a,5) dan (1,3) atau (a,5) dan (-2, -3). Boleh salah satu kok, nanti alhasil sama..
Kita gunakan (a,5) dan (1,3)
x1 = a
y1 = 5
x2 = 1
y2 = 3
Sekarang masuk lagi ke rumus gradien. Ingat gradiennya telah ketemu, yaitu = 2.
Sekarang kita kalikan silang..
- Pindahkan -2a ke ruas kanan sehingga menjadi +2a dan pindahkan -2 ke ruas kiri sehingga menjadi +2.
- Bagi kedua ruas dengan 2 untuk mendapatkan nilai a.