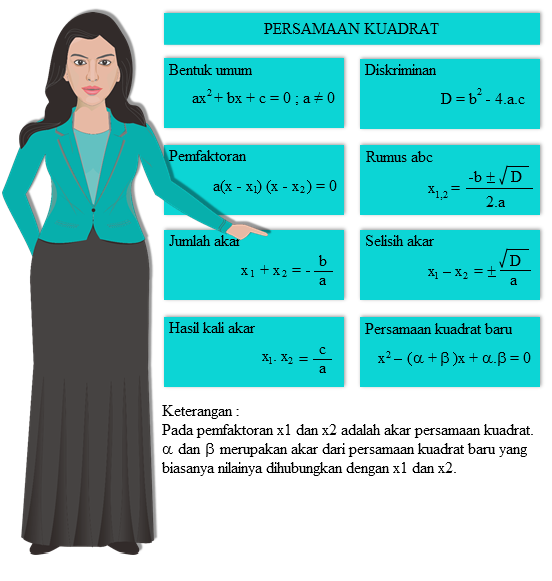
Soal Persamaan Kuadrat

by

Soal Persamaan Kuadrat – Ini memang kami sampikan untuk anda semua alasannya di situs kunci tanggapan akan memperlihatkan pembahasan lengkap bukan cuma materi Soal Persamaan Kuadrat ini saja namun berbagai dari soal Umum, Soal Sekolah Dasar, Soal MI, Soal SMP, Soal MTs, Soal SMA MA, Soal SMK, Hingga Perguruan Tinggi. Tentunya dengan hal ini situs ini akan memberikan kelengkapan buat anda mampu belajari eksklusif untuk materi contoh Soal tersebut.

Untuk Postingan kali ini kami bagikan secara langsung ihwal pembahasan Soal Persamaan Kuadrat sehingga dengan Soal Persamaan Kuadrat ini maka anda bisa eksklusif pelajari soal soal tersebut. Oya untuk situs kunci jawaban juga memberikan Bank Soal yang ada di positingan ini dimana semua artikel dan bahan soal yang kami update saban hari bisa dilihat di artikel Bank Soal yang suda ada di sidebar dan header dari situ ini.

Anda bisa menyaksikan semua soal-soal tersebut lengkap tinggal pilih bahan soal yang anda ingin pelajari. Karena untuk Bank Soal tersebut ialah mencakum semua isi konten di situs kunci tanggapan.

Tidak usa usang-usang maka peroleh Soal Persamaan Kuadrat yang kami posting dibawah ini agar bisa bermainfaat buat anda semua yang dikala ini ingin memelajari Soal Persamaan Kuadrat ini.

Soal Persamaan Kuadrat

Baca Juga :  Soal Fungsi Kuadrat dan Soal akar kuadrat

Soal dan Jawaban Persamaan Kuadrat

  1. Akar-akar persamaan kuadrat 3x2 + 2x – 5 = 0 ialah x1 dan x2. Hitunglah nilai dari 1/x1 + 1/x2.
    Pembahasan 
    Dari persamaan kuadrat di soal dikertahui a = 3, b = 2, dan c = -5.
    x1 + x2 = -b/a
    ⇒ x1 + x2 = -2/3
    x1.x2 = c/a
    ⇒ x1 . x2 = -5/3
    1/x1 + 1/x2 = (x1 + x2) / (x1.x2)
    ⇒ 1/x1 + 1/x2 = (-2/3) / (-5/3)
    ⇒ 1/x1 + 1/x2 = -2/3 . (-3/5)
    ⇒ 1/x1 + 1/x2 = 2/5
    ⇒ 1/x1 + 1/x2 = 0,4.

  2. Jika x1 dan x2 yakni akar-akar dari persamaan kuadrat 2x2 – 6x – p = 0 dan x1 – x2 = 5, maka tentukanlah nilai p. 
    Pembahasan 
    Dari persamaan kuadrat di soal dikertahui a = 2, b = -6, dan c = -p.
    x1 – x2 = (√D) / a
    ⇒ (x1 – x2) a = √D
    ⇒ (x1 – x2) a = √(b2 – 4.a.c)
    ⇒ 5(2) = √(36 – 4.2.(-p)
    ⇒ 10 = √(36 + 8p)
    ⇒ 100 = 36 + 8p
    ⇒ 8p = 64
    ⇒ p = 8.
  1. bila x1 dan x2 ialah akar dari persamaan 32x + 33-2x – 28 = 0, maka tentukanlah jumlah kedua akar tersebut.
    Pembahasan 
    Untuk menuntaskan soal seperti ini, kita perlu mengubah persamaan tersebut menjadi persamaan kuadrat yang sederhana.
    32x + 33-2x – 28 = 0; misalkan 32x = a
    ⇒ 32x + (33)/32x – 28 = 0
    ⇒ a + 27/a – 28 = 0
    ⇒ a2 – 27 – 28a = 0
    ⇒ a2 – 28a – 27 = 0
    ⇒ (a – 1)(a – 27) = 0
    ⇒ a = 1 atau a = 27
    Untuk a = 1, maka :
    32x = a
    ⇒ 32x =1
    ⇒ 32x = 30
    ⇒ 2x = 0
    ⇒ x1 = 0
    Untuk a = 27, maka :
    32x = a
    ⇒ 32x = 27
    ⇒ 32x = 33
    ⇒ 2x = 3
    ⇒ x2 = 3/2
    Makara  x1 + x2 = 0 + 3/2 = 3/2.
  1. Suatu persamaan kuadrat mempunyai akar-akar  x1 dan x2. Jika persamaan kuadrat tersebut adalah 2x2 – 3x – 5 = 0 , maka tentukanlah suatu persamaan kuadrat baru yang akar-akarnya -1/x1 dan -1/x2.
    Pembahasan
    Dari persamaan kuadrat di soal dikenali a = 2, b = -3, dan c = -5.
    x1 + x2 = -b/a
    ⇒ x1 + x2 = -(-3)/2
    ⇒ x1 + x2 = 3/2
    x1.x2 = c/a
    ⇒ x1.x2 = -5/2

    Persamaan kuadrat baru dapat ditentukan dengan rumus :
    x2 – (α + β)x + α.β = 0
    dengan α dan β merupakan akar-akar persamaan kuadrat gres.
    Pada soal diketahui α = -1/ x1  dan β = -1/x2.
    α + β = (-1/x1) + (-1/x2)
    ⇒ α + β = (-1/x1) – (1/x2)
    ⇒ α + β = (-x2 – x1) / (x1.x2)
    ⇒ α + β = – (x1 + x2) / (x1.x2)
    ⇒ α + β = -(3/2) / (-5/2)
    ⇒ α + β = 3/5

    α.β = -1/ x1 . (-1/x2)
    ⇒ α.β = 1/(x1.x2)
    ⇒ α.β = 1/ (-5/2)
    ⇒ α.β = -2/5

    Makara persamaan kuadrat yang akarnya -1/ x1 dan -1/x2 ialah :
    x2 – (α + β)x + α.β = 0
    ⇒ x2 – 3/5x + (-2/5) = 0 
    ⇒ x2 – 3/5x – 2/5 = 0
    ⇒ 5x2 – 3x – 2 = 0.

  1. Suatu persamaan kuadrat x2 – px + p + 1 = 0 mempunyai akar-akar x1 dan x2. Jika dikenali x1 – x2 = 1, tentukanlah nilai p yang menyanggupi persamaan tersebut.
    Pembahasan
    Diketahui : a = 1, b = -p, c = p + 1.
    x1 – x2 = (√D) / a
    ⇒ (x1 – x2) a = √D
    ⇒ (x1 – x2) a= √(b2 – 4.a.c)
    ⇒ 1(1) = √(p2 – 4.1.(p + 1))
    ⇒ 1 = √(p2 – 4p – 4)
    ⇒ 1 = p2 – 4p – 4
    ⇒ p2 – 4p – 5 = 0
    ⇒ (p – 5)(p + 1) = 0
    ⇒ p = 5 atau p = -1.
  1. Akar-akar persamaan kuadrat x2 + 2x + 3 = 0 ialah x1 dan x2. Tentukanlah persamaan kuadrat baru yang memiliki akar-akar (x1 – 2) dan (x2 – 2).

    Rumus Umum Persamaan Kuadrat

    Ini memang kami sampikan untuk anda semua karena di situs kunci jawaban akan memberikan p Soal Persamaan Kuadrat

    Pembahasan
    Dari persamaan kuadrat di soal dimengerti a = 1, b = 2, dan c = 3.
    x1 + x2 = -b/a
    ⇒ x1 + x2 = -2/1
    ⇒ x1 + x2 = -2
    x1.x2 = c/a
    ⇒ x1.x2 = 3/1
    ⇒ x1.x2 = 3

    Persamaan kuadrat baru dapat ditentukan dengan rumus :
    x2 – (α + β)x + α.β = 0
    dengan α dan β merupakan akar-akar persamaan kuadrat baru.
    Pada soal dikenali α = (x1 – 2)  dan β = (x2 – 2).
    α + β = (x1 – 2) + (x2 – 2)
    ⇒ α + β = (x1 + x2) – 4
    ⇒ α + β = -2 – 4
    ⇒ α + β = -6

    α.β = (x1 – 2)(x2 – 2)
    ⇒ α.β = x1.x2 – 2x1 – 2x2 + 4
    ⇒ α.β = x1.x2 – 2(x1 + x2) + 4
    ⇒ α.β = 3 – 2(-2) + 4
    ⇒ α.β = 3 + 4 + 4
    ⇒ α.β = 11

    Kaprikornus persamaan kuadrat yang akarnya (x1 – 2) dan (x2 – 2) adalah :
    x2 – (α + β)x + α.β = 0
    ⇒ x2 – (-6)x + 11 = 0 
    ⇒ x2 + 6x + 11 = 0

sumber:  bahanbelajarsekolah.blogspot.co.id

  Soal Ipa Kelas 5