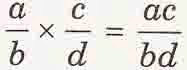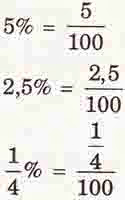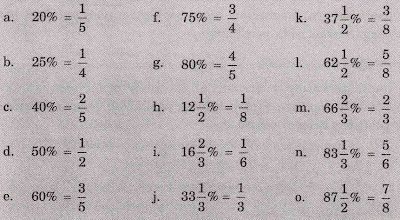Soal Numerik – Tentunya dengan Soal Numerik yang kami sampikan ini akan bisa menciptakan anda mampu memahami dan mengerti Soal Numerik yang kami sampikan untuk anda semua. Soal yang kami berikan juga akan menawarkan pembahasaan dan juga kunci jawabannya sehingga anda tidak butuhkawatir perihal Soal Numerik yang kami sampaikan tersebut.
Ini akan sungguh memudahkan buat anda semua yang ingin berguru Soal Numerik tersebut. Disini admin kunci tanggapan memperlihatkan aneka macam soal-soal dan pembahasan untuk bisa anda pelajari juga sehingga anda mengerti tentang soal yang saat ini anda ingin pelajari.
Untuk selengkapnya perihal Soal Numerik tersebut kamu mampu simak dibawah ini selengkapnya buat anda semua, supaya mampu menjadi manfaat untuk pelajaraan anda ketika ini.
1. BILANGAN
- Bilangan Romawi
| I = 1 (satu) V = 5 (lima) X = 10 (sepuluh) L = 50 (lima puluh) Contoh: |
C = 100 (seratus) D = 500 (lima ratus) M = 1.000 (seribu) MMIII = 2.003 |
- Penjumlahan bilangan bundar
Berikut ini ketentuan operasi penjumlahan bilangan bundar.
- Jika suatu bilangan dijumlahkan dengan lawan bilangannya, maka kesannya yakni nol:
[a + (-a) = 0].
Contoh ⇒ 19 + (-19) = 0, ⇒⇒⇒ -19 musuh dari 1 - Jika suatu bilangan di depannya terdapat tanda negatif lebih besar dari bilangan positifnya, balasannya yakni bilangan negatif.
Contoh ⇒ 8 + (-12) = 8 – 12 = – 4, ⇒⇒⇒ 12 lebih besar dari - Jika suatu bilangan di depannya terdapat tanda negatif lebih kecil dari bilangan positifnya, alhasil ialah bilangan aktual.
Contoh ⇒ (-4) + 14 = 10, ⇒⇒⇒ 4 lebih kecil dari 14
- Pengurangan bilangan bundar
Berikut ini ketentuan operasi pengurangan pada bilangan lingkaran.
- Jika suatu bilangan faktual dikurangi dengan lawannya, maka karenanya dua kali bilangan itu sendiri: [a – (-a) = 2 x a].
Contoh ⇒ 11 – (-11) = 11 + 11 = 22, ⇒⇒⇒ -11 lawan dari 11 - Jika sebuah bilangan negatif dikurangi bilangan positif, karenanya bilangan negatif.
Contoh ⇒ -14 – 6 = -20, ⇒⇒⇒ (sama artinya -14 ditambah -6) - Jika suatu bilangan negatif dikurangi bilangan negatif, ada 3 kemungkinan seperti berikut ini.
Berupa bilangan positif jika bilangan di belakang tanda negatif lebih besar.- Contoh ⇒ -4 – (-9) –4 + 9 = 5, ⇒⇒⇒ 9 lebih besar dari 4
Berupa bilangan negatif bila bilangan di belakang tanda negatif lebih kecil.
- Contoh ⇒ -8 – (-3) = -8 + 3 – -5, ⇒⇒⇒ 3 lebih kecil dari 8
Berupa bilangan nol jika bilangan negatifnya sama.
- Contoh ⇒ -15 – (-15) = -15 + 15 = 0, ⇒⇒⇒ -15 sama dengan -15
- Jika semua bilangan bundar dikurangi dengan nol, balasannya ialah bilangan lingkaran itu sendiri.
Contoh ⇒ 4 – 0 = 4
- Perkalian bilangan bundar
Berikut ini ketentuan operasi perkalian pada bilangan bundar.
- Jika bilangan aktual dikalikan bilangan negatif, akhirnya bilangan negatif.
Contoh ⇒ 6 x (-3) = -15 - Jika bilangan kasatmata dikalikan bilangan konkret, risikonya bilangan positif.
Contoh ⇒ 13 x 5 = 65 - Jika bilangan negatif dikalikan bilangan negatif, hasilnya bilangan konkret.
Contoh ⇒ (-3) x (-7) = 21 - Jika bilangan lingkaran dikalikan dengan nol, risikonya nol.
Contoh ⇒ (-8) x 0 = 0
- Pembagian bilangan lingkaran
Berikut ini ketentuan operasi pembagian pada bilangan bundar.
1. Jika tanda kedua bilangan bulat itu sama
- Positif dibagi konkret jadinya aktual : [ + : + = + ].
Contoh ⇒ 6 : 6 = 1 - Negatif dibagi negatif, akhirnya konkret : [- : – = + ].
Contoh ⇒ (-21) : (-3) = 7
2. Jika tanda kedua bilangan itu berbeda
- Positif dibagi negatif, alhasil negatif: [+ : – = –].
Contoh ⇒ 25 : (-5) = –5 - Negatif dibagi kasatmata, akibatnya negatif: [ – : + = – ].
Contoh ⇒ (-27) : 9 = -3
- Operasi hitung adonan bilangan bulat
- Operasi pembagian dan perkalian yakni sama berpengaruh. Oleh alasannya itu, agar lebih simpel, maka pengerjaan operasi yang ditulis terlebih dahulu mesti dilaksanakan lebih permulaan.
Contoh ⇒ 3 x 4 : 2 = 6
Caranya ⇒ (3 x 4) : 2 = 6 = 12 : 2 - Operasi penjumlahan dan pengurangan sama berpengaruh. Oleh alasannya adalah itu, pembuatan operasi yang ditulis apalagi dahulu harus dijalankan lebih permulaan.
Contoh ⇒ 50 + 25 – 30 = 45
Caranya ⇒ (50 + 25) – 30 = 75 – 30 = 45 - Apabila dalam sebuah soal terdapat tanda kurung, maka pembuatan operasi dalam kurung terlebih dulu mesti dilaksanakan.
Contoh ⇒ 30 : (2 + 4) + 13 = 18
Caranya ⇒ 30 : (6) + 13 = (30 : 6) + 13 = 5 + 13 = 18 - Operasi perkalian dan pembagian lebih besar lengan berkuasa dibandingkan dengan penjumlahan dan pengurangan, maka mesti dilaksanakan apalagi dahulu.
Contoh ⇒ 125 + 400 : 8 – 5 x 30 = 25
Caranya ⇒ 125 + (400 : 8) – (5 x 30) = 125 + 50 – 150 = 175 – 150 = 25
2. PECAHAN
Pecahan memperlihatkan pembagian ½ berarti 1 dibagi 2. Bagian atas sebuah serpihan ialah pembilang, sedangkan bagian bawahnya yaitu penyebut.
- Penjumlahan dan penghematan belahan
- Jika pada penjumlahan atau penghematan pecahan memiliki penyebut sama, maka cukup kerjakan penjumlahan atau pengurangan pada pembilangnya, sementara penyebutnya tetap sama.

- Jika pada penjumlahan atau pengurangan potongan memiliki penyebut yang berlainan, maka terlebih dulu samakan penyebutnya, kemudian mampu dilakukan penjumlahan atau pengurangan pada pembilangnya.
- Perkalian penggalan
Pada perkalian pecahan, Anda tidak perlu menyamakan penyebutnya. Caranya yakni kalikan pembilang dengan pembilang dan penyebut dengan penyebut.
- Pembagian serpihan
Pada pembagian bagian, pembagian belahan pertama dengan bagian kedua sama dengan perkalian kepingan pertama dengan sebalikan dari serpihan kedua.
3. PERSENTASE
Persentase yaitu suatu kepingan yang penyebutnya 100. Untuk mengubah bentuk persentase menjadi bentuk cuilan mampu dikerjakan dengan menuliskan bilangan asli sebagai pembilang dan 100 sebagai penyebut.
Beberapa bentuk persen yang equivalent dengan cuilan dan umum kita kenal yaitu sebagai berikut.
4. PERBANDINGAN
Perbandingan yaitu pernyataan yang membandingkan dua nilai dimana salah satu nilai dibagi nilai lainnya.
Contoh : Di dalam sebuah bus terdapat 15 pria dan 25 perempuan. Perbandingan jumlah laki-laki dengan perempuan dalam bus tersebut ialah atau 15. Perbandingan wanita dengan pria ialah atau 25 : 15. 15
5. PROPORSI
Proporsi yaitu suatu persamaan dari dua penggalan di kedua ruasnya.
Contoh :
Proporsi terbagi menjadi dua, adalah:
- Proporsi eksklusif
Pada proporsi eksklusif, kedua variabelnya berhubungan, artinya jikalau kedua bilangan dikalikan atau dibagi dengan bilangan yang sama, perbandingan tidak berganti.
- Proporsi invers
Pada proporsi invers ada 2 ketentuan, yaitu:
- Peningkatan galah satu nilai melalui perkalian akan mengakibatkan penurunan pada nilai kedua.
- Penurunan salah satu nilai melalui pembagian akan menimbulkan kenaikan pada nilai kedua.
6. RATA-RATA
Rata-rata adalah jumlah bilangan dibagi banyaknya bilangan.
INGAT !!!
- Dalam menuntaskan soal rata-rata, amati satuan yang akan dijumlahkan. Jika berlainan, samakan terlebih dulu, berikutnya dilaksanakan.
- Jika dua atau tiga rata-rata digabung menjadi satu, terlebih dahulu dibentuk bobot yang serupa.
- Jika soalnya menanyakan bilangan yang hilang dengan rata-ratanya tertentu, kurangkan total seluruh bilangan dengan jumlah bilangan yang dikenali.
7. JARAK, WAKTU DAN KECEPATAN
INGAT !!!
- Gunakan rumus yang cocok dengan jawaban yang mau dicari.
- Untuk mengkalkulasikan kecepatan rata-rata dari suatu perjalanan yang terdiri dari dua atau lebih bab, maka anggaplah perjalanan tersebut sebagai satu perjalanan dengan menggunakan total jarak dan total waktu.
- Perhatikan jika ada perbedaan satuan.
- Gambarkan suasana yang diterangkan pada soal.
sumber : soaltpaku.blogspot.co.id