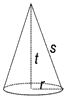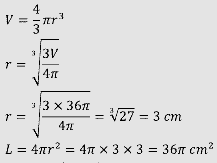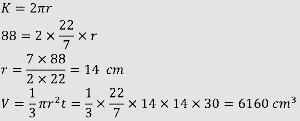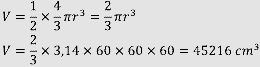Soal Matematika Bangun Ruang Sisi Lengkung – Ini kami sampaikan untuk mampu kau pelajari secara eksklusif perihal Soal Matematika Bangun Ruang Sisi Lengkung dengan Pembahasannya secara pribadi sehingga bagi siswa dan siswi yang ingin mencar ilmu perihal Soal Matematika Bangun Ruang Sisi Lengkung bisa pribadi peroleh dibawah ini, tinggal anda donwload dan pastinya akan bisa menjadi pelajaran yang sangat berharga untuk anda semua untuk bisa berguru Bangun Ruang Sisi Lengkung tersebut.
Yang paling penting jangan perna putus asa ya untuk mampu mencar ilmu Matematikan Bangun Ruang Sisi Lengkung tersebut sebab dengan berguru soal ini anda bisa tahu secara langsung hitungan sisi lengkung benda. Semoga berfaedah untuk Soal Matematika Bangun Ruang Sisi Lengkung peroleh dibawah ini ya selengkapnya.
Soal 1
Sebuah tabung tertutup dengan jari-jari 20 cm dan tingginya 40 cm seperti gbr. berikut.
a) volume tabung d) luas selimut tabung
b) luas ganjal tabung e) luas permukaan tabung
c) luas tutup tabung f) luas permukaan tabung jikalau tutupnya dibuka
Pembahasan soal 1
rumus volum tabung # V = π r2 t
V = 3,14 x 20 x 20 x 40 = 50 240 cm3
b) luas bantalan tabung
Alas tabung berupa bundar sampai rumus luas alasnya menjadi
L = π r2
L = 3,14 x 20 x 20 = 1256 cm2
c) luas tutup tabung
Luas tutup tabung juga berbentuk bulat sama dengan luas ganjal tabungnya.
L = 1256 cm2
d) luas selimut tabung
rumus luas selimut tabung # L = 2 π r t
L = 2 x 3,14 x 20 x 40
L = 5 024 cm2
e) luas permukaan tabung
Luas permukaan tabung merupakan jumlah dari luas selimut, luas bantalan, dan luas tutup tabung
L = 5 024 + 1 256 + 1 256 = 7 536 cm2
atau dengan menggunakan rumus luas pertabung pribadi
L = 2 π r (r + t)
L = 2 x 3,14 x 20 (20 + 40)
L = 12,56 x 60 = 7 536 cm2
f) luas permukaan tabung jika tutupnya dibuka
Soal 2
Sebuah kerucut dengan jari-jari sebesar r = 30 cm dan garis pelukisnya s = 50 cm mirip gbr. berikut.
a) tinggi kerucut c) luas selimut kerucut
b) volume kerucut d) luas permukaan kerucut
Pembahasan Soal 2
a) tinggi dari kerucut
Tinggi kerucut dapat dicari dengan rumus phytagoras dimana
t2 = s2 − r2
t2 = 502 − 302
t2 = 1600
t = √1600 = 40 cm
b) volume kerucut
V = 1/3 π r2 t
V = 1/3 x 3,14 x × 30 x 30 x 40
V = 37 680 cm3
c) luas selimut
Rumus luas selimut kerucur L = π r s
L = 3,14 x 30 x 50
L = 4 710 cm2
d) luas permukaan dari kerucut L = π r (s + r)
L = 3,14 x 30 (50 + 30)
L = 3,14 x 30 x 80 = 7 536 2
Soal 3
Sebuah bola dengan jari-jari sebesar 30 cm mirip pada gambar berikut.
Tentukanlah:
a) volume bola
b) luas permukaan bola
Pembahasan soal 3
a) volume bola
RUmus volum bola # V = 4/3 π r3
V = 4/3 x 3,14 x 30 x 30 x 30
V = 113 040 cm3
b) luas permukaan bola
rumus luas permukaan bola L = 4π r2
L = 4 x 3,14 x 30 x 30
L = 11 304 cm2
Soal 4
Dimiliki sebuah bola besi berada di dalam tabung plastik terbuka di bab atasnya mirip nampak pada gambar berikut.
Tabung tersebut kemudian di isi dengan air sampai sarat . Jika diameter serta tinggi tabung sama dengan diameter dari bola ialah 60 cm, tentukanlah volume air yang telah tertampung oleh tabung!
Pembahasan soal 4
Volume air yang dapat diampung tabung sama dengan volume tabung di minimalisir dengan volume bola yang berada di dalamnya.
dengan rtabung = 30 cm, rbola = 30 cm dan ttabung = 60 cm
V tabung = πr2 t
V tabung = 3,14 x 30 x 30 x 60
V tabung = 169 560 cm3
V bola = 4/3 π r3
V bola = 4/3 x 3,14 x 30 x 30 x 30
V bola = 113 040 cm3
V air = V tabung − V bola
V air = 169 560 − 113 040 = 56 520 cm3
Soal 5
Terdapat dua buah bola dengan jari-jari 10 cm dan 20 cm!
a) Tentukanlah perbandingan volume kedua bola
b) Tentukanlah perbandingan luias permukaan kedua bola
Pembahasan soal 5
a) Perbandingan dari kedua volume bola akan sama dengan perbandingan antara pangkat tiga dari jari-jari masing-masing bola,
V1 : V2 = r13 : r23
V1 : V2 = 10 x 10 x 10 : 20 x 20 x 20 = 1 : 8
b) Perbandingan dari kedua luas permukaan bola akan sama dengan perbandingan dari kuadrat jari-jari masing-masing bola,
L1 : L2 = r12 : r22
L1 : L2 = 10 x 10 : 20 x 20 = 1 : 4
Soal 6
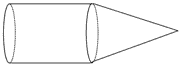
Perhatikanlah gambar dibawah !
Tinggi dan Jari-jari tabung masing-masing 30 cm dan 60 cm, tinggi dari kerucut dan garis pelukisnya masing-masing 40 cm dan 50 cm. Tentukanlah luas permukaan dari berdiri di atas!
Pembahasan soal 6
Bangun diatas yakni gabungan dari tabung tanpa tutup dan kerucut tanpa alas. Cari luasnya masing-masing kemudian jumlahkan.
Luas tabung tanpa tutup = 2π r t + π r2 = (2 x 3,14 x 30 x 60) + (3,14 x 30 x 30) = 11 304 + 2826 = 14130 cm2
Luas selimut kerucut = π r s = 3,14 x 30 x 50 = 4 710 cm2
Luas berdiri = 14130 + 4710 = 18840 cm2
Soal 7
Volume dari sebuah bola yaitu 36π cm3. Tentukanlah luas permukaan dari bola tersebut!
Pembahasan soal 7
Cari dulu jari-jari dari bola dengan rumus volume, setelah di mampu gres mencari luas dari permukaan bola.
Soal 8
Diketahui sebuah kerucut dengan tinggi 30 cm dan mempunyai bantalan dengan keliling 88 cm. Tentukanlah volume kerucut tersebut!
Pembahasan soal 8
Cari jari-jari dari alas kerucut melalui keliling yang sudah dimengerti. Setelah itu mencari volume kerucut seperti soal-soal sebelumnya.
Soal 9
Luas permukaan dari suatu tabung yaitu 2 992 cm2. Jika diketahui diameter bantalan tabung yakni 28 cm, tentukanlah tinggi tabung tersebut!
Pembahasan soal 9
Jari-jari dari ganjal tabung adalah 14 cm, dari rumus luas permukaan mampu di cari tinggi tabung.
Soal 10
Sebuah berdiri berbentuksetengah bola berjari-jari 60 cm mirip nampak gambar berikut.