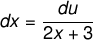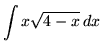Soal Integral

Soal Integral – Ini ialah salah satu hal yang wajib kamu tahu dimana admin blog soal kunci tanggapan memberikan Soal Integral kepada teman-teman semua yang dikala ini mencari Soal Integral, dengan ini maka kau akan tahu selengkapnya pembahasan Soal Integral tersebut. Sehingga para sahabat bisa mengetahui dan memahami Soal Integral yang kami posting buat anda semua disini.

Tentunya ini akan menjadi pelajaran yang sangat berharga sekali buat anda dan admin juga alasannya adalah mempelajari Soal Integral tersebut. Oya di blog Soal dan Kunci Jawaban menawarkan banyak sekali Bank Soal sehingga mempermudah teman-sobat mempelajari Soal-Soal yang keluar di mata pelajaran ketika ini.

Dengan itu semua kami berbagi secara langsung Soal Integral tersebut dibawah ini, tinggal anda copy paste soal yang kami bagi ini, atau juga anda mampu download untuk Soal Integral tersebut.

Sehingga ini akan menjadi mengasyikkan jikalau kita senantiasa belajar Soal Integral dan kamu mampu Soal Integral ini sehingga ditentukan juga teman2 akan mampu mendapatkan Nilai Bagus untuk Soal Integral ini. Ini akan menjadi Bocoran Soal Integral yang harus kau pelajari ketika ini.

Selamat mencar ilmu dan jangan lupa juga senantiasa berdoa duluh sebelum belajar ya supaya otak mampu encer dan bisa menyerap semua Soal Integral yang kami bagikan dibawah ini selengkapnya ok.

y = ( x² + 3x + 5 )⁹ maka turunanya !

Jawab :

y’ = 9 ( x² + 3x + 5 )⁸ ( 2x + 3)

informasi : 
pangkatnya diturukan sehingga dikali 9 dan pangkatnya berganti dari pangkat 9 menjadi 8, ingat yang bagian dalam kurung tetap… lalu dikalikan dengan turunan yang di dalam kurung… turunan  x² + 3x + 5 ialah 2x + 3.

Hal ini memiliki arti :

Lalu..Caranya…??

Misal : u = x² + 3x + 5  maka :

du/dx dibaca turunan fungsi u yang diturunkan variabel x nya….

maka :

teladan soal dan pembahasan integral subtitusi :

       1.    

       Jawab :

(sumber soal : http://www.meetmath.com/161235-materi-integral-subtitusi.html/comment-page-1#comment-423 )


dari dua soal terakhir di atas ada cara praktisnya :

Contoh soal lain :

 1.

misal :

u = x – 1  maka x = u + 1

du/dx = 7  maka dx = du/7

sehingga :

2.

misal :

u = 4 – x  maka x = 4 – u

du/dx = -1 maka dx = du/(-1) = – du

sehingga