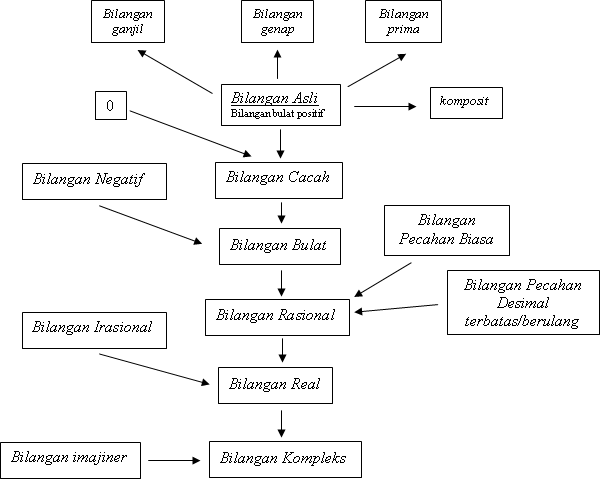
Sejarah Bilangan Real – Media Masyarakat

Untuk memotivasi pembelajaran bilangan real mampu diceritakan secara singkat sejarah bilangan sebagai berikut.

Bilangan selalu muncul akhir keperluan insan. Bilangan yang pertama kali diketahui yaitu bilangan asli. Bilangan ini timbul balasan keperluan manusia untuk mengkalkulasikan. Kemudian timbul bilangan nol, sebuah bilangan yang menyatakan kekosongan. Maka dikenalkan bilangan cacah. Setelah operasi hitung diketahui , timbul bilangan negatif untuk menangani keperluan akan hasil pengurangan dua bilangan asli yang bilangan pertama lebih kecil dari bilangan kedua, maka dikenalkan bilangan bundar. Kemudian untuk mengatasi dilema pembagian dua bilangan yang akhirnya bukan bilangan bulat, diperlukan bilangan rasional. Sedangkan bilangan irasional timbul alasannya adalah adanya operasi pangkat dua, ketika ternyata dimengerti bahwa tidak selalu ada bilangan rasional yang menyanggupi a² = b. Gabungan Bilangan Rasional dan Irasional kemudian disebut bilangan Real. Sekitar abad 16, para mahir matematika mulai memakai bilangan yang mempunyai akar negatif, misalnya dan sebagainya. Maka muncullah himpunan bilangan imajiner. Selanjutnya, bilangan yang terbentuk dari bilangan real dan bilangan imajiner disebut bilangan kompleks.

B. Macam-macam Bilangan

Berikut ini ringkasan materi tentang himpunan-himpunan bilangan.

1. Bilangan orisinil/Natural Numbers

Bilangan asli adalah yang dipakai untuk mengkalkulasikan. Karena dalam mengkalkulasikan kita memulai dengan 1, maka himpunan bilangan asli juga dimulai dari 1, 2, 3, 4,….dan seterusnya.

Simbol yang sering dipakai untuk himpunan bilangan asli yaitu A atau N.

Bilangan asli dibagi menjadi 2 golongan yaitu bilangan genap dan bilangan ganjil. Bilangan genap adalah bilangan yang habis dibagi 2, sedangkan bilangan ganjil tidak habis dibagi 2.

Himpunan bilangan genap yakni G= 2, 4, 6, 8,……………

Himpunan bilangan ganjil yaitu J = 1, 3, 5, 7, ………….

Setiap bilangan asli yang lebih dari 1 dapat dikelompokkan menjadi bilangan prima atau bilangan komposit/tersusun. Sedangkan 1 tidak termasuk keduanya, 1 yakni unit/satuan. Untuk menentukan bilangan prima yang tidak terlampau besar mampu dipakai metode Saringan Erastothenes.

Teorema dasar aritmetika menyatakan bahwa setiap bilangan komposit dapat dinyatakan selaku hasilkali bilangan-bilangan prima. Misalnya 300 dapat dinyatakan dengan 2².3.5². Ini disebut juga faktorisasi prima dari 300.

2. Bilangan Cacah/Whole Numbers

Bilangan cacah ialah semua bilangan asli ditambah dengan 0. Simbol bilangan cacah ialah C.

3. Bilangan bundar/Integers

Bilangan lingkaran ialah semua bilangan cacah ditambah dengan bilangan bulat negatif.

4. Bilangan rasional

Bilangan rasional adalah bilangan yang mampu dinyatakan dalam bentuk p/q, dimana p dan q ialah bilangan bulat dan q ¹ 0. Simbol bilangan rasional yaitu Q.

Jika p habis dibagi q maka bilangan itu adalah bilangan bulat (potongan imitasi), jikalau tidak maka berupa serpihan. Ada 4 macam serpihan yakni serpihan sejati, potongan campuran, serpihan imitasi dan belahan desimal. Bilangan rasional yang dinyatakan dalam bentuk cuilan desimal mampu berbentukdesimal terbatas dan desimal tak terbatas berulang

5. Bilangan irasional

Bilangan irasional adalah bilangan yang tidak dapat dinyatakan dalam bentuk p/q, dimana p dan q ialah bilangan lingkaran dan q ¹ 0.

Bilangan irasional dikenal semenjak sekitar 600 SM di Yunani, dikala orang berusaha mencari penyelesaian dari rumus Pythagoras a²+b²=c² untuk a=1 dan b=1 ternyata tidak ada bilangan rasional yang sempurna untuk c, sebab tidak ada bilangan rasional yang kalau dikalikan dengan dirinya sendiri kesudahannya 2.

Ketika dinyatakan dalam desimal, bilangan irasional adalah desimal yang tak terbatas dan tak berulang. Contoh bilangan Irasional yang menawan yaitu p yaitu bilangan yang didapat dari perbandingan antara keliling dan luas lingkaran.

6. Bilangan Real/Bilangan Nyata

Bilangan real yaitu campuran dari bilangan rasional dan bilangan Irasional. Simbol bilangan real yaitu R.

Operasi hitung pada bilangan real meliputi antara lain penjumlahan, penghematan, perkalian, pembagian, pemangkatan, penarikan akar, dan logaritma.

Sifat tertutup (closure): Jika dilakukan operasi tertentu pada 2 anggota suatu himpunan bilangan dan hasilnya yaitu bilangan yang merupakan anggota himpunan bilangan itu maka dibilang himpunan itu tertutup dalam operasi tersebut.

Contoh:

Dalam himpunan bilangan asli. Operasi penjumlahan bersifat tertutup, namun operasi pengurangan tidak, alasannya 5–7 = -2, dan –2 bukanlah anggota bilangan asli.

Sifat-sifat operasi pada bilangan real diperlihatkan pada tabel berikut.

Untuk a, b, c Î R berlaku:

a. Sifat komutatif pada penjumlahan: a + b = b + a

b. Sifat komutatif pada perkalian: a x b = b x a

c. Sifat asosiatif pada penjumlahan: (a + b) + c = a + (b + c)

d. Sifat asosiatif pada perkalian: (a x b) x c = a x (b x c)

e. Sifat distributif perkalian kepada penjumlahan: ax(b+c)=(axb)+(axc).

Identitas pada penjumlahan yakni 0 sedangkan identitas pada perkalian ialah 1.

Invers penjumlahan yakni lawannya, misalnya invers a yaitu –a.

Invers perkalian yakni kebalikannya, contohnya invers a adalah 1/a

7. Bilangan imajiner

Kata “imajiner” digunakan untuk menggambarkan bilangan mirip Unit imajiner (disimbolkan i) didefinisikan sebagai berikut: i =

dan i² = -1. Selanjutnya didefinisikan akar dari bilangan negatif sebagai berikut: jika a > 0,

8. Bilangan kompleks

Setiap bilangan yang berbentuk a+bi, dimana a dan b yaitu bilangan real dan i ialah unit imajiner, disebut bilangan kompleks.

Contohnya 4i, 3+2i, 2–i, 7 dan 0.

Pada a+bi, a di sebut bab real, dan b disebut bab imajiner. Jika b ≠ 0, maka bilangan tersebut disebut bilangan imajiner.

Pada bilangan imajiner, a+bi, jikalau a = 0, maka disebut bilangan imajiner murni. Contohnya 3i, -i, i dan sebagainya.

Dua bilangan kompleks a+bi dan c+di dikatakan sama, kalau dan cuma jikalau a=c dan b=d.

Contoh Makalah Laporan Pengamatan Proses Persidangan Tindak Kriminal Di Pengadilan Negeri