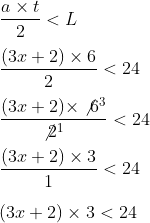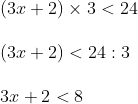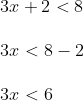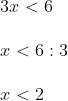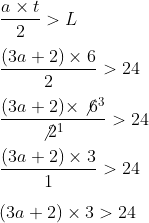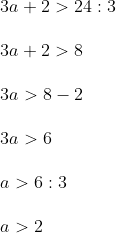Untuk soal ini, kita hanya memerlukan rumus luas segitiga. Tetapi memakai desain pertidaksamaan.
Itu saja bedanya.
Contoh soal
Ok…
Kita masuk ke pola soalnya saja yuk biar pribadi memahami.
Soal :
1. Agar luas segitiga dengan ganjal (3x+2) cm dan tinggi 6 cm kurang dari 24 cm², berapakah batas nilai x?
Diketahui pada soal :
- Alas (a) = 3x+2
- Tinggi (t) = 6 cm
- Luas = 24 cm²
Sekarang kita gunakan rumus luas segitiga.
Masukkan data-data yang dimengerti.
- Pada soal dibilang jika luasnya kurang dari 24.
- Kaprikornus rumus luasnya kita tukar posisi, L di sebelah kanan, sehingga menjadi < L
Terus :
- Masukkan nilai dari bantalan (a) dan tinggi (t)
- Sederhanakan 6 dan 2.
Sama-sama dibagi 2.
- 3 di sebelah kiri berfungsi sebagai pengali.
- Pindahkan 3 ini ke ruas kanan sehingga menjelma pembagi (ketika pindah ruas maka tandanya dibalik, dari pengali menjadi pembagi).
- Pindahkan +2 yang ada di ruas kiri ke ruas kanan menjadi -2
- Untuk menerima x, kita bagi 6 dengan 3.
- Angka di depan x ialah 3, itulah mengapa 6 harus dibagi dengan 3, sesuai dengan angka di depan x
Sehingga diperoleh x < 2.
Inilah nilai x, semoga luasnya kurang dari 24 cm².
Bagaimana kalau luasnya mesti lebih dari 24 cm²?
Soalnya masih mirip, besar luas, alas dan tingginya masih sama seperti soal pertama. Yang membedakan hanyalah luasnya harus lebih dari 24 cm².
Diketahui :
- Alas (a) = (3a+2)
- Tinggi (t) = 6 cm
- Luas (L) = 24 cm²
Sekarang syaratnya diubah menjadi lebih dari 24 cm².
Kemudian :
Nah…
Diperoleh a > 2.
Seperti itulah caranya dan agar menolong ya…
Baca juga ya :