Daftar Isi
Kumpulan Rumus Matematika Volume Bangun Ruang Lengkap
Rumus matematika bangun ruangtelah dipelajari di sekolah dasar (SD) tetapi pada jenjang
SMP materi tentang bangun ruang kembali dipelajari tentu saja lebih detil dibandingkan di tingkat SD. Bangun ruang dibagi dalam dua kategori yaitu bangun ruang sisi lengkung dan bangun ruang sisi datar.
Bangun ruang sisi lengkung terdiri dari :
- Tabung
- Kerucut
- Bola
Bangun ruang sisi datar terdiri dari :
- Kubus
- Balok
- Prisma
- Limas
Rumus Matematika SMP Kelas 9 Tentang Bangun Ruang
Rumus matematika bangun ruang yang akan dibahas disini meliputi volume bangun ruang dan luas permukaan bangun ruang, baik bangun ruang sisi lengkung maupun bangun ruang sisi datar.
Rumus-rumus matematika bangun ruang sisi lengkung
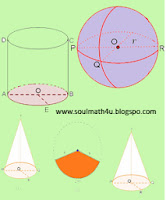
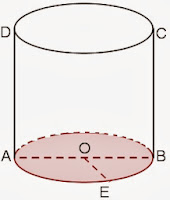
1. TABUNG (tabung)
a.Unsur-unsur pada tabung
Terdiri dari sisi alas , sisi atas (tutup) dan selimut tabung ( s )
OA, OB, OE disebut jari-jari tabung ( r )
AD atau BC disebut tinggi tabung ( t )
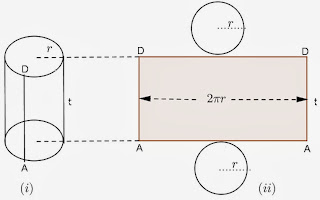
b. Luas Permukaan dan Volume Tabung
Perhatikan gambar jaring-jaring tabung dibawah ini:
dari gambar (ii) diatas, maka rumus luas selimut tabung adalah :
Luas Selimut tabung
Luas Permukaan tabung
Volume Tabung
2. KERUCUT
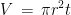
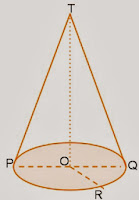
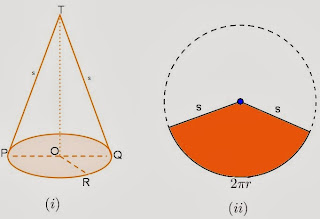
a. Unsur-unsur pada Kerucut
- Terdiri dari sisi alas dan selimut kerucut
- OP, OR, dan OQ disebut jari-jari kerucut dan AB diameter kerucut
- TO adalah garis tinggi, TP = TQ disebut garis pelukis
b. Luas Permukaan dan Volume kerucut
Perhatikan gambar jaring-jaring kerucut dibawah ini,
Dari gambar jaring-jaring kerucut diatas, ternyata selimut kerucut adalah juring lingkaran dengan jari-jari s dan panjang busur 2π r. Maka luas selimut kerucut adalah:
Luas selimut kerucut
Luas Permukaan Kerucut
Volume kerucut
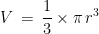
Dan,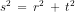 
3.BOLA
a. Unsur-unsur Bola
- OP = OQ = OR = r , adalah jari-jari bola
- PR adalah diameter bola, d = 2 r
b. Luas Permukaan Bola dan Volume Bola
Luas Permukaan Bola
Luas Permukaan Bola
Rumus matematika bangun ruangtentang luas permukaan bola dapat dibuktikan dengan menggunakan prisip integral yaitu pada materi integral luas antara dua kurva pada materi matematika SMA kelas 11.
Volume Bola
Pembuktian rumus matematika bangun ruang khususnya rumus volume bola dapat dibuktikan secara matematis dengan menggunakan prinsip integral yaitu volume benda putar pada materi matematika SMA atau SMK kelas 12.
Rumus-rumus Matematika Bangun Ruang Sisi Datar
Selanjutnya adalah rumus matematika bangun ruang sisi datar, yaitu kubus, balok, prisma dan limas.
1. KUBUS
a. Unsur-unsur pada kubus
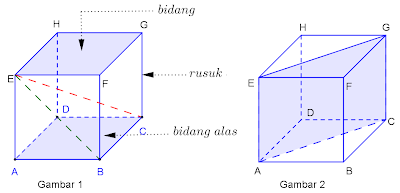
Perhatikan gambar kubus dibawah ini (kubus)
-
Kubus diberi nama berdasarkan bidang alas dan bidang atasnya, dari gambar 1 kubus diberi nama ABCD.EFGH
-
Bidang yaitu yang membatasi bagian luar dan bagian dalam, contoh ABCD, BCGF, dst
-
Rusuk yaitu garis yang membatasi tiap bidang, contoh AB, BC, dst. Semua rusuk kubus sama panjang
-
Diagonal bidang contohnya BE, dst
-
Diagonal ruang contohnya CE , HB, AG, dan DF. Diagonal-diagonal ruang kubus sama panjang
-
Bidang diagonal contohnya Bidang ACGE, bidang BDHF, dst. Bidang diagonal kubus berbentuk persegi panjang
b. Volume Kubus dan Luas permukaan kubus
Volume Kubus
Luas permukaan Kubus
Panjang Diagonal sisi/bidang
Panjang Diagonal Ruang
Luas Bidang diagonal
2. BALOK
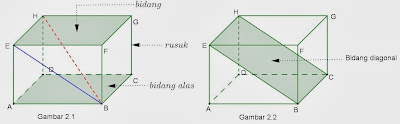
Perhatikan gambar balok dibawah ini :
a. Unsur-unsur pada balok
- Balok diberi nama berdasarkan bidang alas dan bidang atasnya, dari gambar 2.1 balok diberi nama ABCD.EFGH
- Bidang yaitu yang membatasi bagian luar dan bagian dalam, contoh ABCD, BCGF, dst
- Rusuk yaitu garis yang membatasi tiap bidang, contoh AB, BC, dst.
- Diagonal bidang contohnya BE, dst
- Diagonal ruang contohnya HB, CE , AG, dan DF. Diagonal-diagonal ruang balok sama panjang
- Bidang diagonal contohnya Bidang BCEH, bidang ACGE, dst. Bidang diagonal kubus berbentuk persegi panjang
b. Volume Balok dan Luas permukaan Balok
Volume Balok
Luas Permukaan balok
Panjang diagonal ruang balok
3.PRISMA
Sebelum mempelajari rumus matematika bangun ruang tentang prisma, sebaiknya terlebih dahulu kita mengetahui definisi prisma.
Prisma adalah bangun ruang yang dibatasi oleh dua bidang berhadapan yang kongruen dan sejajar, serta bidang-bidang lain yang berpotongan menurut rusuk-rusuk yang sejajar (M. Cholik A & sugijono, MATEMATIKA SMP KELAS VIII Semester 1)
Beberapa contoh prisma :
a.Unsur-unsur Prisma
- Prisma diberi nama sesuai dengan bentuk segi-n pada bidang alas, dari gambar 3 (i) disebut prisma segi empat, gambar 3 (ii) prisma segi tiga, dst.
- Dari gambar 3 (iii) bidang alas prisma ABCDE.EFGHI adalah ABCDE dan bidang atas EFGHI
- Bidang tegaknya ABGF, BCGH, CDHI, dst
- Rusuk tegaknya BG, CH, DI, dst
- Salah satu bidang diagonalnya adalah BEGJ. Bidang diagonal prisma berbentuk persegi panjang
b.Volume Prisma dan Luas Permukaan Prisma
Untuk setiap prisma tegak segi –n berlaku rumus dibawah ini:
Luas permukaan Prisma
Volume Prisma
4. LIMAS
Limas yaitu bangun ruang yang dibatasi sebuah segi – n sebagai alas serta beberapa bidang yang berbentuk segitiga dan bertemu pada satu titik puncaknya. (M.Cholik A & Sugijono, MATEMATIKA SMP KELAS VIII Semester 2)
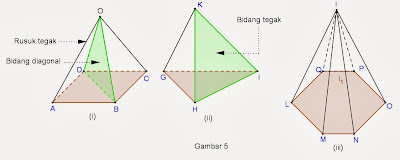
Sebelum mempelajari rumus matematika bangun ruang tentang limas, perhatikan gambar bentuk-bentuk limas dibawah ini :
a. Unsur-unsur Limas
- Cara memberi nama limas sesuai dengan bentuk segi-n pada alasnya. Dari gambar 5 (i) disebut limas segi empat, gambar 5(ii) disebut limas segitiga, dst.
- Bidang tegak limas yaitu KHI, KGH,dst. Gambar 5 (ii)
- Rusuk tegak limas O.ABCD yaitu OA,OB,OC,dst.
- Bidang diagonal limas berbentuk segitiga, lihat gambar 5(i) yaitu bidang OBD
Luas Permukaan Limas
Volume Limas
Untuk setiap limas segi-n selalu berlaku rumus dibawah ini:
Selamat belajar , semoga artikel artikel ini bermanfaaat dan menjadi salah satu sumber referensi rumus matematika bangun ruang.