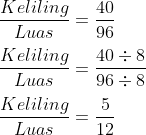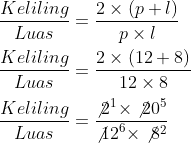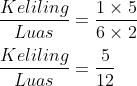Persegi Panjang Ukuran 12 Cm X 8 Cm. Hitunglah Perbandingan Keliling Dan Luasnya!

by

Ketika ukuran suatu persegi panjang diketahui, kita mampu dengan gampang mengkalkulasikan perbandingan keliling dan luasnya.

Langkah-langkahnya

Ada dua langkah yang bisa dicoba dan alhasil sama. Jadi bisa diseleksi cara mana yang lebih disukai atau dirasa lebih gampang.

Untuk yang pertama yakni mencari masing-masing nilai dari keliling dan luas. Setelah itu dibandingkan mirip biasa.
Perbandingan mewajibkan kita mempersempit.

Sederhanakan sampai ketemu angka yang paling kecil

Angka yang tidak mampu dibagi lagi.

Sedangkan yang kedua, kita eksklusif memasukkan angkanya pada perbandingan rumus, sehingga lebih mempersingkat perkiraan.
Dan pastinya lebih cepat.

Nah..
Pasti lebih senang dengan yang singkat dan cepat bukan?
Ok, mari teruskan.

Menghitung perbandingannya

Seperti yang sudah disebutkan di atas, ada dua cara yang mampu dicoba dan kini kita kerjakan satu per satu.
Mari mulai.

Soal :

1. Persegi panjang mempunyai ukuran 12 cm x 8 cm. Hitunglah perbandingan keliling dan luasnya!

Cara pertama

Hitung keliling dan luasnya.

Keliling = 2×(p + l)
  • p = 12cm
  • l = 8 cm
Keliling = 2×(12+8)
  • lakukan yang di dalam kurung dulu
  • 12 + 8 = 20
Keliling = 2×20
Keliling = 40.
Luas = p × l
Luas = 12 × 8
Luas = 96.
Sekarang kita bandingkan keduanya.
Masukkan nilai keliling dan luas
40 dan 96 disederhanakan dengan sama-sama membagi 8
Kita dapatkan perbandingannya 5 : 12.
Itulah akhirnya.
Cara kedua

Untuk cara yang kedua mirip dengan yang pertama, tetapi kita langsung memasukkan rumus keliling dan luas ke dalam perbandingannya.

Masukkan rumus keliling dan luas
Ganti panjang dan lebarnya
Jumlahkan 12 + 8 yang di dalam kurung dulu menjadi 20
Untuk luas, jangan dikalikan.
Kemudian bagi 2 dan 12, sama-sama dibagi 2.
Bagi 20 dan 8 sama-sama dibagi 4
Nah…
Akhirnya kita mendapatkan bentuk yang lebih sederhana, yakni 5 : 12.
Inilah perbandingan dari keliling dan luas persegi panjang tersebut.
Gunakan cara kedua
Untuk menerima perbandingan dari suatu nilai, seharusnya memang menggunakan cara yang kedua. 
Mengapa?
Karena jauh lebih gampang dan cepat.
Kita tidak perlu lagi mencari nilai dari keliling dan luas.
Langsung memasukkan rumus dan mulai mencoret bagian mana yang bisa disederhanakan. Jauh lebih cepat dan ringkas.
Untuk cara pertama, kita harus mencari keliling dan luasnya secara terpisah. Setelah diperoleh angkanya, baru disederhanakan.
Dua kali kerja.
Nah…
Jika ada yang lebih cepat dan ringkas, mengapa harus ribet.
Gunakan cara kedua.
Masukkan rumus dan angka yang dimengerti. Langsung bagi angka yang mampu dibagi dan hasil yang paling sederhana mampu pribadi diperoleh.
Semoga menolong.
Baca juga ya :
  Fungsi Linear