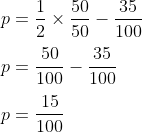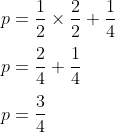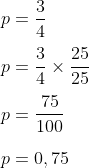Kita bisa menyelesaikan soalnya dengan membuat seluruh soal menjadi bentuk desimal ataupun serpihan. Dan jawabannya juga bisa berbentuk cuilan atau desimal.
Soal
Baik…
Kita lakukan soalnya.
Soal :
1. Jika p + 0,35 = ½, maka hitunglah nilai p!
Tulis lagi soalnya.
p + 0,35 = ½
- Untuk mendapatkan p, maka ½ harus dikurangkan dengan 0,35
p = ½ – 0,35
- Ubah 0,35 menjadi bentuk bagian, yaitu = ³⁵/₁₀₀
p = ½ – ³⁵/₁₀₀
- Samakan penyebutnya.
- 2 bisa menjadi 100 dengan mengalikan 50
Menjadi desimal
Jawaban yang diperoleh mampu diubah menjadi dua bentuk, ialah desimal dan kepingan paling sederhana. Kita ubah ke desimal dahulu.
p = ¹⁵/₁₀₀
- Dibagi 100 artinya ada dua angka di belakang tanda koma
- Pembilang cuma ada dua angka saja, yaitu 15 (1 dan 5)
- Kaprikornus, di depannya mesti diberikan pemanis angka 0.
p = 0,15
Inilah tanggapan yang pertama.
Menjadi kepingan sederhana
p = ¹⁵/₁₀₀ mampu disederhanakan lagi.
Bagi pembilang dan penyebut dengan angka yang sama, yaitu 5.
p = ¹⁵/₁₀₀
- 15 dibagi 5 = 3
- 100 dibagi 5 = 20
Sehingga kita dapatkan penggalan paling sederhananya adalah p = ³/₂₀.
Soal :
2. p – ¼ = ½, Hitunglah nilai p!
Masih menggunakan konsep yang sama. Di sini kita akan mencari nilai a memakai bentuk pecahan.
p – ¼ = ½
- Untuk menerima p, maka ½ harus dijumlahkan dengan ¼
p = ½+¼
- Penyebut kedua serpihan adalah 2 dan 4.
- KPKnya yaitu 4.
- Jadi ½ dikalikan dengan 2/2
- Sedangkan 1/4 tetap, tidak perlu dikali lagi alasannya adalah penyebutnya sudah 4.
Itulah balasan pertamanya dalam bentuk belahan.
p = ¾
Bentuk desimal
Sekarang ubah ¾ menjadi bentuk desimal.
- Penyebutnya yakni 4.
- Untuk menjadi desimal, maka penyebutnya mesti menjadi 10 atau 100.
- 4 bisa dijadikan 100 dengan mengalikan 25.
- Kalikan pembilang dan penyebutnya dengan 25.
Kemudian :
- Kita menerima 75/100
- Untuk mengubah ke desimal, memiliki arti harus ada dua angka di belakang koma alasannya dibagi 100.
Sehingga desimalnya ialah 0,75.
Nah…
Itulah cara mencari nilai p dari masing-masing bentuk penjumlahan dan penghematan bagian.
Baca juga ya :