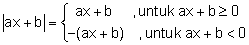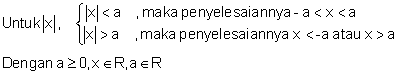Menyelesaikan Persamaan Mutlak
Nilai mutlak sebuah bilangan dapat diartikan jarak antara bilangan tersebut dr titik nol(0). Dengan demikian jarak selalu bernilai positif.
Misalnya:
Parhatikan garis bilangan berikut.
Jarak angka 6 dr titik 0 ialah 6
Jarak angka -6 dr titik 0 ialah 6
jarak angka -3 dr titik 0 yaitu 3
Jarak angka 3 dr titik0 ialah 3.
Dari penjelesan di atas memang tampak bahwa nilai mutlak sebuah bilangan senantiasa bernilai konkret.
Berkaitan dgn memilih nilai mutlak sebuah bilangan, maka muncullah tanda mutlak. Tanda mutlak disimbolkan dengan garis 2 ditepi sebuah bilangan atau bentuk aljabar.
Misalnya seperti berikut.
Secara umum, bentuk persamaan nilai mutlak dapat dimaknai seperti berikut.
Jika kita mempunyai persamaan dlm bentuk aljabar, maka mampu dimaknai selaku berikut.
Makara, bentuk dasar di atas dpat digunakan untuk membantu menuntaskan persamaan mutlak.
Lebih jelasnya amati acuan-contoh berikut.
Contoh
Tentukan himpunan solusi dr persamaan nilai Mutlak di bawah ini.
Jawaban:
Bentuk-Bentuk persamaan nilai mutlak di atas mampu dituntaskan sebagai berikut. Pada prinsipnya, langkah langkah penyelesaian nilai mutlak diusahakan bentuk mutlak berada di ruas kiri.
1. Pada bentuk ini ada dua penyelesaian.
(*) x + 5 = 3 , maka x = 3 – 5 = -2
(**) x + 5 = -3, maka x = -3 – 5 = -8
Kaprikornus, himpunan penyelesaiannya yakni -2, -8
2. Pada bentuk ini ada dua solusi.
(*) 2x + 3 = 5 , maka 2x = 5 – 3
2x = 2 <==> x = 1
(**) 2x + 3 = -5 , maka 2x = -5 -3
2x = -8 <==> x = -4
Makara, himpunan penyelesaiannya yaitu -4, 1
3. Perhatikan bentuk aljabar di dlm tanda mutlak, yaitu x+1. Penyelesaian persamaan nilai mutlak ini pula dibagi menjadi dua potongan.
Bagian pertama untuk batasan x+1>= 0 atau x >= -1
Bagian kedua untuk batas-batas x+1< 0 atau x < -1
Mari kita tuntaskan.
(*) untuk x >=-1
Persamaan mutlak mampu ditulis:
(x + 1) + 2x = 7
3x = 7 – 1
3x = 6
x = 2 (terpenuhi, karena batasan >= -1)
(**) untuk x < -1
Persamaan mutlak dapat ditulis:
-(x + 1) + 2x = 7
-x – 1 + 2x = 7
x = 7 + 1
x = 8 (tidak terpenuhi, sebab batas-batas < -1)
Kaprikornus, Himpunan penyelesaiannya ialah 2 .
4.
Perhatikan bentuk aljabar di dlm tanda mutlak, yaitu 3x + 4. Penyelesaian persamaan nilai mutlak ini pula dibagi menjadi dua kepingan.
Bagian pertama untuk batasan 3x+4>= 0 atau x >= -4/3
Bagian kedua untuk batasan 3x+4< 0 atau x < -4/3
Mari kita tuntaskan.
(*) untuk x >=-4/3
Persamaan mutlak mampu ditulis:
(3x + 4) = x – 8
3x – x = -8 – 4
2x =-12
x = -6 (tidak terpenuhi, karena batasan >= -4/3)
(**) untuk x < -4/3
Persamaan mutlak dapat ditulis:
-(3x + 4) = x – 8
-3x – 4 = x -8
-3x – x = -8 + 4
-4x = -4
x = 1 (tidak tercukupi, alasannya batasan < -4/3)
Jadi, Tidak ada Himpunan penyelesaiannya.
Menyelesaikan Pertidaksamaan Nilai Mutlak
Menyelesaikan pertidaksamaan nilai mutlak caranya hampir sama dgn persamaan nilai mutlak. cuma saja berbeda sedikit pada tanda ketidaksamaannya. Langkah-langkah berikutnya seperti menuntaskan pertidaksamaan linear atau kuadrat satu variabel .
Pertidaksamaan mutlak dapat digambarkan selaku berikut.
Apabila fungsi di dlm nilai mutlak berbentuk ax + b maka pertidaksamaan nilai mutlak mampu dituntaskan seperti berikut.

Lebih jelasnya perhatikan contoh berikut ini.
Contoh
Tentukan himpunan penyelesaian dr Pertidaksamaan nilai mutlak berikut ini.
Jawaban
1. Cara menyelesaikan pertidaksamaan mutlak ini selaku berikut.
-9 < x+7 < 9
-9 – 7 < x < 9 - 7
-16 < x < 2
Makara, himpunan penyelesaiannya yakni x/ -16 < x < 2
2. Cara menyelesaikan pertidaksamaan mutlak ini dibagi menjadi dua penggalan.
(*) 2x – 1 >= 7
2x >= 7 + 1
2x >= 8
x >= 4
(**) 2x – 1 <= -7
2x <= -7 + 1
2x <= -6
x <= -3
Jadi, himpunan penyelesaiannya ialah x/ x <= -3 atau x >= 4
3. Kalau dlm bentuk soal ini, langkah menyelesaikan pertidaksamaannya dgn mengkuadratkan kedua ruas.
amati proses berikut ini.