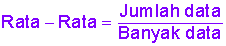Menentukan Rata-Rata
Dalam menentukan rata-rata suatu data, kita mesti pandai menjumlah & membagi apalagi dahulu. Rata-Rata data dirumuskan sebagai berikut.
Perhatikan pola berikut.
1. Nilai sepuluh siswa dlm ulangan Matematika sebagai berikut.
9 7 5 6 8 9 7 9 5 8
Tentukan Rata-rata nilai siswa.
Jawaban :
Jumlah nilai = 9 + 7 + 5 + 6 + 8 + 9 + 7 + 9 + 5 + 8 = 73
Banyak siswa = 10
Rata-Rata = 73/10 = 7,3
Kaprikornus, nilai rata-rata siswa yakni 7,3.
2. Perhatikan berat ayam dlm tabel berikut.
|
Berat Ayam (ons)
|
Banyak
|
|
21
|
5
|
|
24
|
3
|
|
26
|
4
|
|
27
|
3
|
|
29
|
1
|
Tentukan rata-rata berat setiap ayam.
Jawaban :
Tabel pada soal dapat dilengkapi sebagai berikut.
|
Berat Ayam (ons)
|
Banyak
|
Berat x Banyak
|
|
21
|
5
|
105
|
|
24
|
3
|
72
|
|
26
|
4
|
104
|
|
27
|
3
|
81
|
|
29
|
1
|
29
|
|
Jumlah
|
16
|
391
|
Jumlah seluruh berat ayam = 391
Banyak ayam = 16
Rata-Rata = 391/16 =24,4375
Jadi, rata-rata berat setiap ayam adalah 24,4375 ons.
3. Perhatikan diagram berikut.
Diagram berikut menghidangkan wacana hasil tangkapan ikan dr para nelayan. 
3. Perhatikan diagram berikut.
Diagram berikut menghidangkan wacana hasil tangkapan ikan dr para nelayan.
Tentukan rata-rata hasil tangkapan setiap ikan.
Jawaban:
Hasil tangkapan ikan
Tengiri = 60 kg
Bawal = 80 kg
Kakap = 50 kg
Layur = 65 kg
Tongkol = 90 kg
Jumlah = 345 kg
Rata-Rata = 345/5 = 69
Makara, rata-rata hasil tangkapan setiap ikan sebanyak 69 kg.
Menentukan Median (Nilai Tengah)
Median yaitu nilai tengah suatu data sehabis nilai-nilai data (datum) tersebut diurutkan (dari yg terkecil).
Jika kita mempunyai data nilai data berikut : 6 4 7 9 5 6 7 (banyak datum ganjil)
Data tersebut dapat diurutkan menjadi : 4 5 6 6 7 7 9
Nilai data yg di tengah adalah 6.
Jadi mediannya yakni 6.
Jika kita mempunyai data nilai data berikut : 20 28 24 30 22 30 (banyak datum genap)
Data tersebut dapat diurutkan menjadi : 20 22 24 28 30 30
Nilai data yg di tengah antara 24 & 28.
Nilai yg ada di tengah-tengah 24 & 28 dapat dijumlah (24+28)/2 = 52/2 = 26.
Kaprikornus mediannya adalah 26.
Secara lazim, Median suatu data dapat dirumuskan :
Menentukan Modus
Modus ialah nilai data yg paling banyak atau paling kerap muncul.
Jika kita mempunyai data nilai data berikut : 4 4 4 5 5 5 6 6 6 6 6 7 7 8 8 8 8 9 9
Nilai 4 muncul 3 kali
Nilai 5 muncul 3 kali
Nilai 6 timbul 5 kali
Nilai 7 timbul 2 kali
Nilai 8 timbul 4 kali
Nilai 9 timbul 2 kali
Tampak bahwa nilai 6 timbul paling banyak, yakni 5 kali.
Kaprikornus, modus data tersebut yakni 6.
Untuk memperdalam, perhatikan beberapa pola berikut.
1. Diketahui berat badan sekelompok siswa (dalam kg) sebagai berikut.
45 48 50 56 43 48 58 65 60 50
44 52 49 65 56 58 54 48 59 60
Tentukan median & modus dari data di atas.
Jawaban :
Data diiurutkan dr yg terkecil.
43 44 45 48 48 48 49 50 50 52
54 56 56 58 58 59 60 60 65 65
Banyak datum ada 20.
Median terletak diantara 52 & 54. Sehingga nilai diantara 52 & 54 ialah (52+54)/2 = 53.
Kaprikornus, median ialah 53 kg.
Perhatikan bahwa berat badan 48 timbul sebanyak 3 kali (paling banyak)
Jaadi, modusnya yaitu 48 kg.
2. Perhatikan tabel wacana nilai ulangan Matematika berikut.
|
Nilai
|
Banyak Siswa
|
|
60
65
68
76
80
95
|
4
7
2
5
4
3
|
Tentukan median & modus dr data tersebut.
Jawaban :
Banyak datum ada 25.
Median terletak pada datum ke 13.
Berdasarkan tabel di atas, datum ke 13 terletak pada nilai 68.
|
Nilai
|
Banyak Siswa
|
Jumlah kumulatif
|
|
60
65
68
76
80
95
|
4
7
2
5
4
3
|
4
11
13
18
22
25
|
Menentukan Gradien Garis dan Persamaan Garis Lurus
Kaprikornus, median yaitu 68.
Berdasarkan tabel di atas terlihat bahwa siswa terbanyak memiliki nilai 65.
Makara, modusnya adalah 65.
3. Perhatikan diagram batang wacana nilai berikut.
