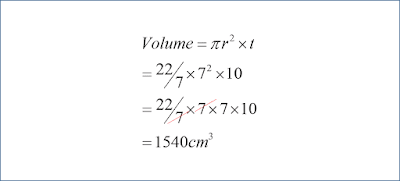Karena yang diketahui yaitu keliling alas dan juga tingginya, maka yang menjadi standar kita dalam memecahkan soal ini yaitu keliling bantalan.
Ok, kita eksklusif saja cek soalnya ya..
Contoh soal :
1. Suatu tabung memiliki keliling ganjal 44 cm dan tinggi 10 cm. Berapakah volume dari tabung tersebut? (π = 22/7)
1. Suatu tabung memiliki keliling ganjal 44 cm dan tinggi 10 cm. Berapakah volume dari tabung tersebut? (π = 22/7)
Yuk kita cari jawabannya..
Langkah 1 => analisa soal
Kita amati yang diketahui :
- Keliling alas = 44 cm
- tinggi = 10 cm
Dari apa yang diketahui, hanyalah keliling ganjal yang bisa dicari dengan memakai rumus.
Keliling bantalan inilah yang mau menjadi titik permulaan kita untuk mencari bagian lain yang belum dimengerti dalam tabung ini, yakni jari-jari (r).
Langkah 2 => Mencari jari-jari
Keliling alas tabung berbentuk bundar, maka kita akan menggunakan rumus keliling dari lingkaran.
Keliling alas = 2πr
r = jari-jari
Sekarang amati perhitungannya..
- Ganti nilai dari keliling dengan 44
- π diganti dengan 22/7
- Sekarang tinggal mencari r saja.
- Perhatikan baris paling atas, di depan “r” masih ada bilangan 44/7
- Untuk menerima nilai dari “r”, maka angka di depannya haruslah 1
- Kaprikornus untuk memperoleh 1, maka ruas kanan haruslah dibagi dengan 44/7 juga (dibagi dengan bilangan yang serupa di depan r)
- Di ruas sebelah kiri pun mesti dibagi dengan 44/7
- Perhatikan ruas kiri!! Ketika 44 : 44/7, maka tanda bagi berubah menjadi kali dan 44/7 ditukar posisinya sehingga dikali dengan 7/44.
- Diperoleh r = 7 cm.
Langkah 3 => Mencari volume
Volume tabung = πr2 x t
r = 7 cm
t = tinggi tabung = 10 cm
Sekarang masuk ke rumusnya..
Nah selesai..
Volume tabung yang dicari telah diperoleh..
Baca juga :