Relasi matematika ialah hubungan antara dua buah himpunan dan namanya bisa ditentukan dengan menyaksikan tanda panah yang sudah dibuat.
Dan kini kita akan menjajal menemukan nama relasi tersebut.
Berikut misalnya..
Cara membaca sebuah relasi ialah mengikuti tanda panahnya. Jika pada korelasi diatas, panahnya dimulai dari kiri (A) dan menuju ke kanan (B), membacanya ialah himpunan A adalah …… himpunan B.
Mari kita teruskan..
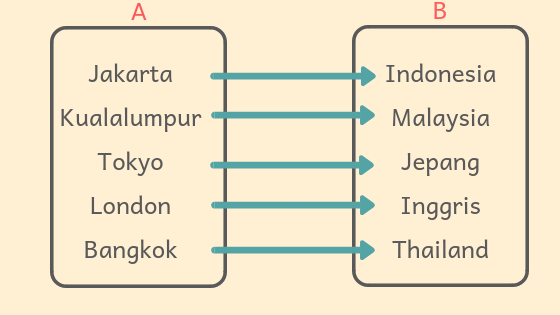
Kaprikornus relasinya dibaca seperti ini :
- Jakarta yaitu …… Indonesia
- Kualalumpur yaitu ….. Malaysia
- Tokyo ialah …. Jepang
- London adalah …. Inggris
- Bangkok yaitu ….. Thailand
Yang sempurna untuk mengisi titik-titik tersebut ialah “ibukota dari“
Kaprikornus kekerabatan diatas ialah hubungan dengan nama “ibukota dari”
Bagaimana, mudah bukan??
Untuk menemukan nama suatu kekerabatan, semua anggota dalam himpunan A itu mesti memenuhi syarat “ibukota dari”.
Jika saja ada satu bab himpunan A yang tidak cocok, nama relasinya bukan seperti diatas. Harus dicari lagi yang lain yang cocok.
Nah, untuk soal yang satu ini sungguh ibarat dengan soal pertama, tapi ada satu bagian di himpunan A yang berlawanan.
Yaitu “Osaka”
Sekarang kita tidak mampu memakai korelasi “ibukota dari” untuk menyatakan hubungan himpunan A dan B.
Mengapa tidak bisa memakai “ibukota dari”?
Karena dibagian A, Osaka dihubungkan ke Jepang dan Ibukota Jepang sendiri yakni Tokyo.
Makara tidak pas jikalau kita gunakan relasi “ibukota dari”.
Relasi yang lebih sempurna yakni “kota yang ada di” atau “kota populer di” atau “kota besar di”
Nah, mudah bukan??
Mari kita selidiki satu per satu..
Kita mulai dari himpunan A ke himpunan B sesuai panahnya.
- 2 yaitu ….4
- 3 ialah…..5
- 4 yaitu ….6
- 5 yakni ….7
- 6 yakni ….8
Kira-kira apa yang pas untuk mengisi titik-titik tersebut??
Yang pas ialah..
“dua kurangnya dari”.
Sehingga :
- 2 yakni dua kurangnya dari 4
- 3 yaitu dua kurangnya dari 5
- 4 adalah dua kurangnya dari 6
- 5 yakni dua kurangnya dari 7
- 6 yakni dua kurangnya dari 8
- 2 yaitu … 4
- 3 adalah … 6
- 4 yakni … 8
- 5 yakni … 10
- 6 ialah … 12
Hubungan yang sempurna yaitu “dua kalinya dari”
Silahkan dicocokkan ya..