Mencari Luas Persegi Panjang Yang Ukurannya (√5 + 1) dan (√5 – 1)

by

Ketika mencari luas persegi panjang, tinggal gunakan saja rumus biasanya dan hasilnya bisa eksklusif diperoleh.

Contohnya seperti soal dibawah ini..

Soal :

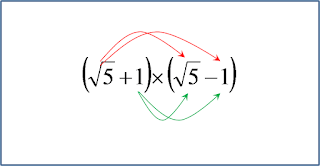
1. Sebuah persegi panjang memiliki panjang (√5 + 1) cm dan lebar (√5 – 1) cm. Berapakah luas dan kelilingnya?

Kita cari luasnya dahulu..

Luas

Rumus luas persegi panjang = panjang × lebar

Diketahui :

  • panjang  = √5 + 1
  • lebar  = √5 – 1
Sehingga :
Luas = panjang × lebar
Luas = (√5 + 1) ×  (√5 – 1)
Langkahnya seperti ini :
  • Kalikan √5 dengan √5, sehingga akibatnya = 5
  • Kalikan √5 dengan -1, sehingga kesannya = -√5
  • Kalikan 1 dengan √5, sehingga hasilnya = +√5
  • Kalikan 1 dengan -1, sehingga akibatnya = -1

Jadi, kita menjadikannya :
Luas = 5 – √5 + √5 – 1
  • -√5 + √5 = 0
Luas = 5 – 1
Luas = 4 cm²
Keliling

Rumus keliling yakni 2 dikali dengan penjumlahan panjang dan lebar..

Atau..

Keliling = 2 × ( panjang + lebar)

Diketahui :

  • panjang = √5 + 1
  • lebar = √5 – 1

Masukkan ke dalam rumus panjang dan lebarnya..

Keliling = 2 × ( panjang + lebar)

Keliling = 2 × ( √5 + 1 + √5 – 1)

  • +1 – 1 = 0

Keliling = 2 × ( 2√5 )

Keliling = 4√5 cm..

Bagaimana, mudah bukan?

Ingat ya cara mengalikan bentuk dari akar seperti diatas..

Soal :

2. Sebuah persegi panjang memiliki panjang (√6 + 2) cm dan lebar (√6 – 2) cm. Berapakah luas dan kelilingnya?

Langkahnya sama dengan soal pertama..

Luas

Diketahui :

  • panjang  = √6 + 2
  • lebar  = √6 – 2
Sehingga :
Luas = panjang × lebar
Luas = (√6 + 2) ×  (√6 – 2)

Langkahnya seperti ini :
  • Kalikan √6 dengan √6, sehingga jadinya = 6
  • Kalikan √6 dengan -2, sehingga jadinya = -2√6
  • Kalikan 2 dengan √6, sehingga kesudahannya = +2√6
  • Kalikan 2 dengan -2, sehingga alhasil = -4
Sehingga :

  Soal dan Pembahasan Bangun Datar Segitiga Kelas VII
Luas = 6 – 2√6 + 2√6 – 4
  • -2√6 + 2√6 = 0
Luas = 6 – 4
Luas = 2 cm²
Keliling

Keliling = 2 × ( panjang + lebar)

Diketahui :

  • panjang = √6 + 2
  • lebar = √6 – 2

Masukkan ke dalam rumus panjang dan lebarnya..

Keliling = 2 × ( panjang + lebar)

Keliling = 2 × ( √6 + 2 + √6 – 2)

  • +2 – 2 = 0

Keliling = 2 × ( 2√6 )

Keliling = 4√6 cm..

Penggunaan sifat distributif perkalian
Sifat distributif perkalian sangatlah berguna dalam menyelesaikan soal seperti ini. Tolong diketahui caranya ya.
Rajin berlatih niscaya mengetahui.
Terus, soalnya telah dikondisikan.
Maksudnya begini.
Soal sudah dirancang sedemikian manis, tetapi terlihat rumit di permulaan. Padahal hasilnya bilangan bundar tanpa ada akar.
Nah…
Kita mesti terpelajar dan teliti.
Jangan langsung mundur dan tidak inginmencoba dikala berjumpa dengan soal seperti ini ya. Coba saja dahulu dan telusuri prosesnya.
Ketika bertemu jawabannya, pasti merasa puas.
Kaprikornus, pahami sifat perkaliannya dan silahkan coba soalnya.