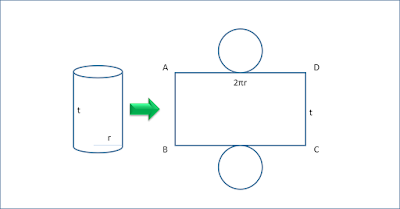
Mencari Luas Permukaan Tabung Jika Diketahui Jari-jari dan Tingginya

by

Cara yang bagus untuk mencari luas sebuah bangun ruang yakni membelah bangkit tersebut. Kemudian dipecah-pecah dan dicari satu-satu.



Sehingga kita lebih gampang memahami dalam mencari rumus luasnya.

Contoh soal

Mari perhatikan acuan soal dibawah ini..

Contoh soal

 1. Sebuah tabung mempunyai jari-jari alas 7 cm dan tinggi 10 cm. Berapakah luas seluruh permukaan tabung tersebut?


Nah, perhatikan langkah demi langkah dalam menuntaskan soal ini..

Langkah 1 => analisa soal



Tabung jikalau dibelah, maka akan menghasilkan mirip gambar diatas.

Tabung berisikan :

  • 2 buah bundar, bantalan dan tutup
  • Selimut dengan panjang “2πr” dan berbentuk persegi panjang, lebarnya adalah tinggi tabung (t).
Kaprikornus untuk mencari luas total tabung, tinggal jumlahkan saja ke-tiga bangun tersebut dan ketemulah luasnya.

Untuk luas selimut bagaimana?

Selimut tabung berbentuk persegi panjang :
  • panjangnya sendiri sama dengan keliling bulat (2πr). 
  • Lebarnya sama dengan tinggi tabung itu sendiri (t).
Luas selimut tabung = 2πr x t

                                 = 2πrt



Langkah 2 => Menghitung luasnya


Untuk mendapatkan luas tabung, kita mesti mencari luas bundar dan juga luas selimutnya.

r = 7 cm
t = 10 cm


Luas bundar = πr2
           
= 22/7 x 7 x 7

= 154 cm2 

Luas selimut = 2πrt
= 2 x 22/7 x 7 x 10

 = 440 cm2   


Luas permukaan tabung berisikan dua lingkaran dan satu selimut, sehingga :

 Luas permukaan tabung = (2 x luas bulat) + ( luas selimut tabung)

 = (2 x 154) + ( 440)

 =   308 + 440

 =   748 cm2    

  Kerucut tingginya 20 cm dan diameternya 7 cm. Berapakah volumenya?


Kaprikornus luas permukaan tabung yang kita cari yaitu 748 cm2.   

Cara lain


Untuk yang ini kita akan memakai rumus eksklusif. Tabung termasuk berdiri ruang yang memiliki alas dan tutup, jadi rumus ini melakukan pekerjaan dengan baik untuknya.

Rumus :
Luas permukaan = (2×Luas bantalan) + (Keliling alas × tinggi)

Masukkan rumus luas dan keliling ganjal pada rumus.
Alas tabung adalah lingkaran, jadi keliling yang dipakai pastinya keliling bundar juga ya.

Luas permukaan = (2×Luas ganjal) + (Keliling alas × tinggi)
Luas permukaan = (2×πr²) + (2πr × t)
Luas permukaan = 2πr² + 2πrt

Kedua suku sama-sama mengandung 2πr, sehingga rumusnya mampu diubah menjadi berikut.
2πr² dibagi 2πr menyisakan r
2πrt dibagi 2πr menyisihkan t

Luas permukaan = 2πr(r+t)


Nah, inilah rumus yang akan  membantu kita.


Menghitung luasnya


Sekarang masukkan data yang dimengerti pada soal.

r = 7 cm
t = 10 cm
π = ²²∕₇ (Karena jari-jari (r) bisa dibagi 7)

Luas permukaan = 2πr(r+t)
Luas permukaan = 2×(²²∕₇)×7×(7+10)
  • ²²∕₇×7
  • Kedua 7 bisa dicoret sehingga bersisa 22 saja.

Luas permukaan = 2×22×(17)
Luas permukaan = 748 cm²

Hasilnya sama dengan cara pertama.
Semoga menolong


Baca juga ya :