Mencari Banyaknya Bola Yang Bisa Dimasukkan Ke Dalam Suatu Tabung

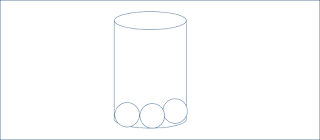
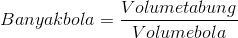Dan kini ceritanya akan dimasukkan beberapa bola dengan ukuran tertentu ke dalam tabung yang memiliki ukuran tertentu juga.

Jangan galau dahulu..
Nanti akan dijelaskan cara-caranya dan andapun niscaya akan memahami dengan gampang..

Lihat soalnya

Pertanyaan yang berhubungan dengan persoalan ini ialah selaku berikut..

Contoh soal :

1. Suatu tabung mempunyai diameter 12 cm dan tinggi 9 cm. Ke dalam tabung ini akan dimasukkan beberapa buah bola yang memiliki jari-jari 3 cm.

Berapakah banyak bola yang bisa masuk ke dalam tabung tersebut?

Mari kita evaluasi dulu soalnya..

Langkah 1 ⇒ Analisa soal

Tujuan utama dari soal ini ialah mencari berapa banyak bola yang masuk ke dalam tabung.

Praktis sekali..
Benar sangatlah mudah..

Untuk mendapatkan berapa banyak bola yang mampu masuk ke dalam tabung, caranya yaitu dengan membagi volume yang lebih besar dengan volume yang lebih kecil.

• Volume lebih besar yakni tabung
• Volume lebih kecil pastinya bola (sebab dimasukkan ke dalam tabung)

Nah, inilah kunci dari soal mirip ini..

Langkah 2 ⇒ Menyelesaikan soal

---

Karena sudah dikenali rumusnya, maka sekarang kita mampu eksklusif mencari banyak bola yang masuk ke dalam tabung..

Penjelasan dari rumus diatas yakni seperti dibawah ini..

Tabung :

• Diketahui diameter 12 cm, maka jari-jari (r) = 6 cm. (diameter : 2)
• tinggi tabung = 9 cm

Bola :

• Jari-jari (r) telah diketahui 3 cm.

Sekarang masuk ke rumusnya.

• π dibiarkan saja seperti itu, sebab nanti akan dibagi dan hilang. Jika diganti dengan angka, mampu membuat ribet. Percayalah!!
• Rumus tabung yaitu π x r ² x tinggi
• Rumus bola ialah 4/3 x π x r ³. (lihat diatas biar lebih terperinci)

Lanjutan :

Tips penting!!

• π tidak usah diganti dengan angka 3,14 atau 22/7. Biarkan saja seperti itu alasannya adalah pada hasilnya akan dibagi dan hilang.
• Cara ini khusus berlaku jika membagi dua volume dan juga mencari perbandingan.

Selamat mencoba dan semoga membantu..