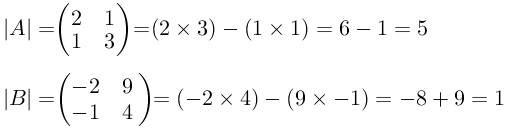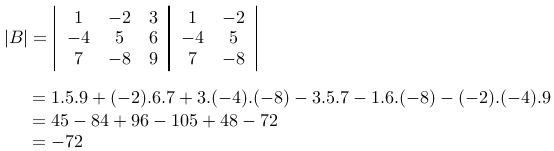Invers Matriks – Media Masyarakat

Daftar Isi

Rumus Invers Matriks Matematika SMA dan SMK

Invers matriks persegi atau bujur sangkar baik yang berordo 2×2, 3×3 , maupun ordo n x n akan menjadi topik pembahasan kali ini. Sebelum mempelajari invers matriks, terlebih dahulu akan dibahas tentang determinan matriks.

Determinan Matriks Ordo 2×2

Jika $A=\left ( \begin{matrix} a &b \\ c & d \end{matrix} \right )$ suatu matriks persegi yang berordo 2×2, maka determinan matriks A ditulis |A| atau det A adalah:

$\left | A \right |=ad-bc$

Contoh mencari determinan matriks ordo 2×2

Diketahui matriks-matriks dibawah ini:

Tentukan | A | dan | B |

[Penyelesaian]

Determinan matriks A dan B adalah,

Syarat dua Matriks Saling Invers

Diketahui A dan B dua buah matriks persegi yang berordo sama sehingga AB = BA = I , maka B adalah invers dari A ditulis B = $A^{-1}$ dan A adalah invers dari B ditulis A = $B^{-1}$ . Maka,

http://soulmath4u.blogspot.com/2014/03/invers-matriks.html

Contoh dua matriks saling invers:

Diketahui matriks-matriks dibawah ini,

Tunjukkan bahwa AB = BA = I

[Penyelesaian]

Hasil kali matriks AB adalah,

Hasil kali matriks BA adalah,

Matriks Singular dan Matriks Non Singular

Matriks singular adalah matriks yang determinannya nol, dan matriks non singular adalah matriks yang determinan nya tidak nol

Contoh matriks singular

Diketahui matriks dibawah ini,

Buktikan bahwa A adalah matriks singular!

[Penyelesaian]

Determinan matriks A adalah,

Rumus invers matriks 2×2

Jika $A=\left ( \begin{matrix} a &b \\ c & d \end{matrix} \right )$ , maka $A^{-1}$ adalah,

Dari rumus invers matriks diatas dapat disimpulkan bahwa:

(a). Suatu matriks persegi atau bujur sangkar tidak memiliki invers jika dan hanya jika matriks persegi tersebut singular

(b). Suatu matriks persegi atau bujur sangkar memiliki invers jika dan hanya jika matriks persegi tersebut non singular.

Invers Matriks 2×2 Contoh Soal dan Pembahasan

Tentukan invers matriks dibawah ini!

(1). $A=\left ( \begin{matrix} 3 & 4\\1 &2 \end{matrix} \right )$

[Penyelesaian]

$\\A^{-1}=\frac{1}{\left | A \right |}\left ( \begin{matrix} d & -b\\ -c &a \end{matrix} \right ) \\\\=\frac{1}{3.2-4.1}\left ( \begin{matrix} 2 &-4 \\-1 &3 \end{matrix} \right )$
$\\=\frac{1}{2}\left ( \begin{matrix} 2 &-4 \\-1 &3 \end{matrix} \right ) \\\\=\mathbf{\left ( \begin{matrix} 1 &-2 \\ -\frac{1}{2} &\frac{3}{2} \end{matrix} \right )}$

(2). $B=\left ( \begin{matrix} 5 &-8 \\4 &-6 \end{matrix} \right )$

[Penyelesaian]

$\\B^{-1}=\frac{1}{5.(-6)-(-8).4}\left ( \begin{matrix} -6 &8 \\-4 & 5 \end{matrix} \right )=\frac{1}{-30+32}\left ( \begin{matrix} -6 &8 \\-4 & 5 \end{matrix} \right ) \\\\\\B^{-1}=\frac{1}{2}\left ( \begin{matrix} -6 &8 \\-4 & 5 \end{matrix} \right ) =\left ( \begin{matrix} -3 &4 \\ -2 & \frac{5}{2} \end{matrix} \right )$

(3). $P=\left ( \begin{matrix} 2 &6 \\ -1 &-3 \end{matrix} \right )$

[Penyelesaian]

$\\\left | P \right |=2.(-3)-6.(-1) \\\\\left | P \right |=-6+6=0$

Determinan P = 0 jadi invers P tidak ada.

(4). $A=\left ( \begin{matrix} 2 &4 \\3 &7 \end{matrix} \right )\, \, dan\, \, B=\left ( \begin{matrix} 4 & 10\\ 5 &3 \end{matrix} \right )$ Tentukan Matriks C jika AC = B

[Penyelesaian]

Kalikan kedua ruas dengan $A^{-1}$ dari kiri,
$\\\Leftrightarrow A^{-1}.AC=A^{-1}.B \\\\\Leftrightarrow C=A^{-1}.B\, .....(1)$
Dari (1),
$\\C=\frac{1}{2}\left ( \begin{matrix} 7 &-4 \\ -3 &2 \end{matrix} \right )\left ( \begin{matrix} 4 & 10\\ 5 &3 \end{matrix} \right ) \\\\C=\frac{1}{2}\left ( \begin{matrix} 8 & 58\\-2 & -24 \end{matrix} \right )=\left ( \begin{matrix} 4 & 29\\-1 & -12 \end{matrix} \right )$

(5).Diketahui dua buah matriks, $P=\left ( \begin{matrix} 4 & -1\\6 & -2 \end{matrix} \right )\, \, dan\, \, Q=\left ( \begin{matrix} a & x\\ b & c \end{matrix} \right )$ Jika invers P sama dengan transpose Q tentukan x

[Penyelesaian]

$\\\Leftrightarrow P^{-1}=Q^{t} \\\\\Leftrightarrow -\frac{1}{2}\left ( \begin{matrix} -2 &1 \\ -6 & 4 \end{matrix} \right )=\left ( \begin{matrix} a &b \\ x &c \end{matrix} \right ) \\\\\Leftrightarrow \left ( \begin{matrix} 1 &-\frac{1}{2} \\3 & -2 \end{matrix} \right )=\left ( \begin{matrix} a &b \\ x &c \end{matrix} \right )$
Berdasarkan elemen yang seletak maka x = 3

Dari contoh-contoh diatas dapat disimpulkan bahwa invers matriks tidak selalu ada, bergantung pada determinannya.

Invers Matriks 3×3

Cara menentukan invers matriks selain ordo 2×2 dapat menggunakan adjoint matriks. Jadi sebelum mempelajari cara mencari invers matriks ordo 3×3, terlebih dahulu harus dipelajari tentang minor, kofaktor, dan adjoint.

1.Minor

Jika pada matriks A ordo 3×3 elemen baris ke-i dan kolom ke-j dihilangkan maka akan didapat matriks yang baru dengan ordo 2×2, determinan matriks baru dengan ordo 2×2 itulah yang disebut minorditulis dengan simbol $\left | M_{ij} \right |$ . Agar lebih jelas perhatikan contoh dibawah ini,

Jika diketahui matriks A ordo 3×3 ,

Maka minor-minor dari matriks A adalah , $\left | M_{11} \right |$

, hilangkan baris ke-1 dan kolom ke-1 matriks A diatas maka sisanya adalah elemen-elemen di dalam kotak merah dibawah ini

Sehingga mminor dari $\left | M_{11} \right |$ adalah :

$\left | M_{12} \right |$ , hilangkan baris ke-1 dan kolom ke-2 matriks A diatas maka :

$\left | M_{32} \right |$ , hilangkan baris ke-3 dan kolom ke-2 matriks A diatas maka:

⋮

Dst

Jadi, minor dari matriks A adalah:

2.Kofaktor

Kofaktordituliskan dengan simbol $A_{ij}$ dibaca kofaktor baris ke-i dan kolom ke-j dan rumus nya adalah :

Jika diketahui matriks A,

Dari rumus kofaktor diatas maka kofaktor-kofaktor dari matriks A diatas adalah:

Jadi, kofaktor dari matriks A adalah,

Agar lebih jelas perhatikan contoh dibawah ini!

Contoh 1

Diketahui matriks A yaitu,

Tentukan minor dan kofaktor dari matriks A

[Penyelesaian]

(a). Minor-minor dari matriks A adalah,

Minor-minor dari matriks A lainnya adalah ,

Jadi, matriks minornya adalah:

(b). Kofaktor-kofaktor matriks A adalah:

Jadi, matriks kofaktornya adalah:

3.Adjoint

Adjoint suatu matriks diperoleh dari transpose matriks kofaktornya. Pemahaman anda tentang adjoint, minor, determinan dan kofaktor sangat dibutuhkan dalam menentukan invers matriks ordo 3×3

4. Determinan Matriks ordo 3×3

Untuk menentukan determinan matriks ordo 3×3 menggunakan metode sarrus. Perhatikan contoh dibawah ini,

Jika matriks B diketahui seperti dibawah ini,