Daftar Isi
Pengertian Matriks Matematika SMA , Ordo Dan Notasi Matriks
a. Pengertian Matriks
Matriks adalah susunan kelompok bilangan yang disusun atau diatur dalam baris dan kolom berbentuk persegi atau persegi panjang. Susunan bilangan tersebut diletakkan dalam tanda kurung biasa ( ), kurung siku [ ], atau garis tegak ganda || ||.
Istilah-istilah Penting dalam matriks
a.Nama suatu matriks ditulis menggunakan huruf kapital seperti A, P, D, …
b.Baris suatu matriks adalah bagian susunan bilangan yang ditulis mendatar (horizontal)
c. Kolom suatu matriks adalah bagian susunan bilangan yang ditulis tegak (vertikal)
d. Elemen atau unsur suatu matriks bilangan-bilangan penyusun matriks
e.Dalam matriks )
dengan i dan j anggota bilangan asli, bilangan )
disebut elemen matriks .
f.Dalam penulisan indeks ganda, indeks i menunjukkan baris dan indeks j menunjukkan kolom
Contoh matriks:
Diketahui matriks berikut,
Tentukanlah:
a) banyak baris dan kolom matriks A
b) Elemen baris ke-1, elemen baris ke-3 , elemen kolom ke-2 dan elemen kolom ke-3
c)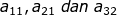 
[Penyelesaian]
a) Banyak baris = 3, dan banyak kolom = 4
b) Elemen baris ke-1 adalah 1, 4, –1 , dan 0
Elemen baris ke-3 adalah – 1, 0 , –2, dan 1
Elemen kolom ke-2 adalah 4, –3, dan 0
Elemen kolom ke-3 adalah –1, –5, dan –2
c)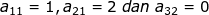 
b.Ordo Matriks
Ordo (ukuran) matriks adalah banyaknya baris dan kolom suatu matriks.
Matriks 
berarti matriks A berordo m × n, yang artinya matriks A mempunyai m buah baris dan n buah kolom.
Contoh:
Tentukan ordo matriks berikut ini!
[Penyelesaian]
a. Ordo matriks P adalah 3 × 3
b. Ordo matriks B adalah 3 × 4
Jenis-jenis Matriks
a. Matriks persegi yaitu matriks yang jumlah barisnya sama dengan jumlah kolom atau matriks berordo m × m. Contoh,
Matriks A disebut matriks persegi ordo 2 × 2, elemen 1 dan –3 disebut diagonal utama (DU), dan elemen 2 dan 4 disebut diagonal samping (DS).
Coba anda tentukan ordo matriks B termasuk diagonal utama dan diagonal samping nya!
b. Matriks baris, yaitu matriks yang terdiri dari satu baris. Contoh,
M = (3 2 6 ) dan N = ( 5 4 –1 5 7 )
c. Matriks kolom, yaitu matriks yang terdiri dari satu baris. Contoh,
d. Matriks nol, yaitu matriks yang setiap elemennya nol. Contoh,
e. Matriks segitiga, yaitu matriks persegi yang elemen-elemen dibawah atau diatas diagonal utama seluruhnya nol. Contoh,
Matriks S disebut matriks segitiga atas dan matriks T disebut matriks segitiga bawah
f.Matriks diagonal, yaitu matriks persegi yang semua elemennya kecuali elemen-elemen pada diagonal utama adalah nol. Contoh,
Matriks S disebut matriks diagonal ordo 3 × 3
g.Matriks skalar, yaitu matriks diagonal yang elemen-elemen pada diagonal utama semuanya sama. Contoh,
h.Matriks identitas, atau matriks satuan adalah matriks diagonal yang semua unsur diagonal utamanya adalah 1, dilambangkan dengan hutuf I. Contoh,
i. Matriks simetris, yaitu matriks persegi yang elemen pada baris ke-i kolom ke- jsama dengan baris ke- j kolom ke-i, sehingga 
. Contoh, 
Matriks B disebut matriks simetris ordo 3 × 3
j.Matriks mendatar, yaitu matriks yang jumlah barisnya lebih kecil dari jumlah kolomnya. Contoh,
Matriks B adalah matriks mendatar berordo 2 × 4
k.Matriks tegak, yaitu matriks yang jumlah barisnya lebih besar dari jumlah kolomnya. Contoh,
Matriks C adalah matriks tegak berordo 4 × 2
Transpose Matriks
Matriks transpose adalah matriks ordo n × m yang diperoleh dari penukaran baris dengan kolom matriks , dilambangkan dengan 
(baca : A transpose)
Contoh:
Diketahui matriks C, tentukan transpose matriks C. 
[Penyelesaian]
Kesamaan Dua Matriks
Matriks A dan B dikatakan sama jika dan hanya jika, ordonya sama dan nilai tiap elemen yang seletak juga sama.
Contoh :
1. Tentukanlah nilai x dan y dan z dalam kesamaan matriks dibawah ini!
[Penyelesaian]
Berdasarkan prinsip kesamaan dua matriks, maka diperoleh
2.Diketahui matriks-matriks dibawah ini, Jika 
, tentukan nilai a,b,c,d,e dan f
[Penyelesaian]
Tentukan terlebih dahulu 
,
Dari kesamaan diatas diperoleh,
Dua buah matriks A dan B dapat dijumlahkan jika matriks A dan B memiliki ordo yang sama. Hasil penjumlahan matriks A dan B adalah matriks baru yang berordo sama dengan matriks A dan B yang elemen-elemenya didapat dari hasil menjumlahkan elemen-elemen seletak pada matriks A dan B.
Contoh soal penjumlahan matriks:
1. Diketahui matriks-matriks dibawah ini:
Tentukan jumlah matriks A dan matriks B
[Penyelesaian]
Jumlah matriks A dan B adalah,
2.Diketahui matriks-matriks dibawah ini:
Jika A + B = C, tentukan nilai-nilai dari p, q, r dan s.
[Penyelesaian]
Tentukan terlebih dahulu persamaan yang memenuhi A + B = C,
Dari ….(1),
3p – 1 = –2, maka p = – 1/3
4q + 2 = –4, maka q = – 3/2
3r – 2 = 5, maka r = 7/3
–2s – 2 =6, maka s = –4
Pengurangan matriks
Jika A dan B dua buah matriks yang ordonya sama, maka A – B = A+(– B). Sehingga,
Contoh:
Diketahui matriks-matriks berikut ini:
Tentukan A – B
[Penyelesaian]
Dari prinsip pengurangan matriks, maka diperoleh:
Sifat-sifat Operasi Penjumlahan Matriks
Jika A, B, C dan D matriks-matriks yang berordo sama maka berlaku sifat-sifat penjumlahan matriks dibawah ini:
1) (A + B) + C = A + (B + C) (sifat asosiatif)
2) A + B = B + A (sifat komutatif)
3) A + O = O + A = A
4) terdapat matriks P , sehingga A + P = B
Lawan suatu Matriks
Jika A dan B dua buah matriks yang berordo sama dan A + B = 0 , maka matriks A adalah lawan dari matriks B begitu juga sebaliknya.
Contoh :
Diketahui matriks dibawah ini,
Tentukan lawan dari matriks P
[Penyelesaian]
Lawan dari matriks P = –P maka,
Perkalian Bilangan real dengan Matriks
Jika k suatu bilangan real dan P matriks ordo m × n , k P merupakan matriks ordo m × n dan elemen-elemennya merupakan elemen setiap matriks P dikalikan dengan k.
Contoh :
Tentukanlah nilai a, b, c, dan d dari soal dibawah ini,
[Penyelesaian]
Selesaikan terlebih dahulu persamaan matriks diatas,
Dari (1) diatas:
2a – 6 = 6 , maka a = 6
2b + 3 = 0 , maka b = – 3/2
2c + 12 = 0 , maka c = – 6
2d – 3 = 6 , maka d = 9/2
Demikian pembahasan materi tentang matriks, tinggalkan kritik dan saran anda dibagian komentar. Jangan lupa like fanspage facebook nya, Semoga bermanfaat.
Materi Terkait