Fungsi, Komposisi Fungsi dan Fungsi Invers (1)

A. Fungsi

Fungsi, atau disebut pula pemetaan, merupakan suatu kekerabatan yg khusus. Fungsi/pemetaan dr himpunan A ke himpunan B ialah kekerabatan khusus yg memasangkan setiap anggota A, dgn sempurna satu anggota B. Dengan demikian, setiap anggota himpunan A memiliki sempurna satu kawan dgn anggota himpunan B. Jadi, fungi telah pasti suatu korelasi, namun korelasi belum tentu suatu fungsi.

Misalkan f yaitu suatu fungsi yg memetakan x anggota A ke y anggota B, maka fungsi f dapat dinotasikan selaku berikut:

Jika x anggota himpunan A & y anggota himpunan B, serta fungsi f memetakan x ke y, maka y merupakan peta/bayangan dr x. Pada fungsi tersebut, himpunan A disebut tempat asal atau domain (D_f), himpunan B disebut daerah mitra atau kodomain (K_f), sedangkan himpunan semua peta A di B disebut kawasan hasil atau range (R_f).

Jenis-jenis fungsi & macam-macam fungsi sesungguhnya ada banyak, misalkan fungsi konstan, fungsi identitas, fungsi linear, fungsi kuadrat, fungsi genap & fungsi ganjil, fungsi modulus, fungsi eksponen, fungsi logaritma, maupun fungsi tangga. Namun pada potensi ini kita tak membahas jenis-jenis fungsi tersebut. Di sini akan konsentrasi membicarakan pada fungsi komposisi & fungsi invers.

B. Fungsi Komposisi

Aljabar Fungsi
Sebelum membahas komposisi fungsi, mari mengulang lagi tentang sifat-sifat fungsi aljabar.
Jika f(x) & g(x) yaitu fungsi-fungsi aljabar yg terdefinisi, maka berlaku sifat-sifat fungsi aljabar berikut.
1. (f + g)(x) = f(x) + g(x)
2. (f – g)(x) = f(x) – g(x)
3. (f . g)(x) = f(x) . g(x)
4. (f /g)(x) = f(x) / g(x) , g(x) tak sama dgn 0
5. fⁿ(x) = [f(x)]ⁿ

Contoh 1
Diketahui f(x) = 2x + 1, g(x) = x² – 2, & h(x) = 4x.
Tentukan
a. (f +g)(x)
b. (f – g)(x)
c. f.g(x), dan
d. (f/g)(x).

Jawaban:
a. (f + g)(x) = f(x) + g(x)
                   = (2x + 1) + (x² – 2)
   = x² + 2x – 1
b. (f – g)(x) = f(x) – g(x)
                   = (2x + 1) – (x² – 2)
   = –x² + 2x + 3
c. f.g(x) = f(x) . g(x)
= (2x + 1) (x² – 2)
              = 2x³ – 4x + x² – 2
              = 2x³ + x² – 4x – 2
d. f/g(x) = f(x)/g(x)
                = (2x + 1)/(x² – 2)

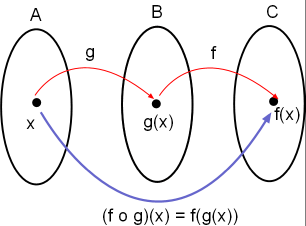
Aturan Sinus dan Aturan Kosinus (Konsep Trigonometri Bagian 2)

Komposisi Fungsi

Misalkan f ialah suatu fungsi dr A ke B & g adalah fungsi dr B ke C , maka suatu fungsi h dr A ke C disebut fungsi komposisi.

Fungsi komposisi tersebut dinyatakan dgn h(x) = g o f (x) (dibaca: g bundaran f)

Secara grafik, komposisi fungsi di atas digambarkan mirip berikut.

Untuk lebih jelasnya, perhatikan beberapa pola berikut.

Contoh 2

Diketahui fungsi f(x) = 3x – 5 & g(x) = 2x + 1.

Tentukan:

a. (f o g)(x)

b. (g o f)(x)

c. (f o g)(2)

d. (g o f)(6)

Jawaban:

a. (f o g)(x) = f (g(x))                     = 3 g(x) – 5
                     = 3(2x + 1) – 5
                     = 6x + 3 – 5
                     = 6x – 2

b. (g o f)(x) = g (f(x))
                    = 2 f(x) + 1
                    = 2(3x – 5) + 1
                    = 6x – 10 + 1
                    = 6x – 9

c. (f o g)(x) = 6x – 2
(f o g)(2) = 6 x 2 – 2
= 12 – 2
= 10

d. (g o f)(x) = 6x -9
(g o f)(6) = 6 x 6 – 9
= 36 – 9
= 27

Contoh 3
Diketahui f(x) = 3x + 2 & g(x) = x² + 2x – 1
Tentukan:
a. (f o g)(x)

b. (g o f)(x)

c. (f o g)(2)

d. (g o f)(-3)

Cara Menentukan Bayangan Titik dan Kurva oleh Transformasi Geometri (Translasi)

Jawaban:
a.      (f o g)(x) = f ((gx))
   = 3 g(x) + 2
   = 3 (x² + 2x – 1) + 2
   = 3x² + 6x – 3 + 2
                         = 3x² + 6x – 1

b.      (g o f)(x) = g(f(x))
                         = (f(x))² + 2(f(x)) – 1
   = (3x + 2)² + 2(3x + 2) – 1
   = 9x² + 14x + 4 + 6x + 4 – 1
                         = 9x² + 20x + 7

c. (f o g)(2) = 3. 2² + 6.2 – 1
= 12 + 12 – 1
= 23

d.      (g o f)(-3) = 9(-3)² + 20(-3) + 7
   = 81 – 60 + 7
   = 28

Sekarang bagaimana jikalau menentukan fungsi yg di depan atau di belakang dr komposisi fungsi yg dimengerti & salah satu fungsi pembentuknya pula dimengerti?
Misalkan f o g(x) diketahui & f(x) diketahui, bagaimana menentukan g(x)?
atau
Misalkan f o g(x) dikenali & g(x) dikenali, bagaimana memilih f(x)?

Mari kita diskusikan dgn beberapa acuan berikut.

dr himpunan A ke himpunan B adalah relasi khusus yg memasangkan setiap anggota A Fungsi, Komposisi Fungsi & Fungsi Invers (1)

Contoh 4
Diketahui (f o g)(x) = 6x + 7 & f(x) = 2x + 3. Tentukan fungsi g(x).

Jawaban:
Caranya, substitusikan g(x) ke dlm f(x) sehingga diperoleh bentuk berikut.
(f o g)(x) = 6x + 7 atau ditulis:
f(g(x)) = 6x + 7
2.g(x) + 3 = 6x + 7
      2.g(x) = 6x + 7 – 3
      2.g(x) = 6x + 4
   g(x) = (6x + 4) /2
         g(x) = 3x + 2
Makara, fungsi g(x) = 3x + 2

Cara Menentukan penyelesaian Persamaan Kuadrat Bentuk ax2 + bx + c = 0

Contoh 5
Diketahui (f o g)(x) = 3x + 2 & g(x) = x + 5. Tentukan fungsi f(x).

Jawaban:
Caranya, dgn memisalkan t = g(x), sehingga di tulis:
t = x + 5, kemudian nyatakan x dlm t menjadi x = t – 5.
Dengan demikian diperoleh bentuk gres mirip berikut.
f (g(x)) = 3x + 2
substitusikan (gantilah) g(x) dgn t & gantilah x dgn t – 5.
f(t) = 3(t – 5) + 2
= 3t – 15 + 2
= 3t – 13
Kembalikan lagi ke fungsi dlm x yaitu f(x) .
f(x) = 3x – 13
Jadi, fungsi f(x) = 3x – 13

Contoh 6
Diketahui (f o g)(x) = 6x² + 2x – 1 dan f(x) = 2x + 1. Tentukan fungsi g(x).

Jawaban:
Caranya, substitusikan g(x) ke dlm f(x) sehingga diperoleh bentuk berikut.
(f o g)(x) = 6x² + 2x – 1 atau ditulis:

f(g(x)) = 6x² + 2x – 1.
2.g(x) + 1 = 6x² + 2x – 1
      2.g(x) = 6x² + 2x – 1 – 1
      2.g(x) = 6x² + 2x – 2
   g(x) = (6x² + 2x – 2) /2
         g(x) = 3x² + x – 1
Jadi, fungsi g(x) = 3x² + x – 1

Contoh 7
Diketahui (f o g)(x) = 6x² + 2x + 5 dan g(x) = x + 3. Tentukan fungsi f(x).

Jawaban:
Caranya, dgn memisalkan t = g(x) terlebih dahulu.
Sehingga diperoleh bentuk: t = x + 3 atau dgn membalik bentuk dlm t diperoleh x = t – 3.
Selanjutnya gantilah permasalahan di atas dlm variabel t.

(f o g)(x) = 6x² + 2x + 5
f(g(x)) = 6x² + 2x + 5.
f(t) = 6(t – 3)² + 2(t – 3) + 5
f(t) = 6(t² – 6t + 9) + 2(t – 3) + 5
f(t) = 6t² – 36t + 54 + 2t – 6 + 5

f(t) = 6t² – 36t + 2t + 54 – 6 + 5
f(t) = 6t² – 34t + 53
Sehingga dgn mengubah t menjadi x, diperoleh:
f(x) = 6x² – 34x + 53

Kaprikornus, fungsi f(x) = 6x² – 34x + 53.

Itulah sekilas pengetahuan tentang fungsi & fungsi komposisi.

Mari kita lanjutkan dengan fungsi invers & invers fungsi