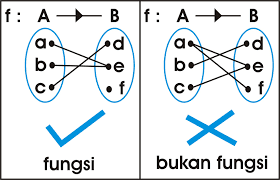
Fungsi Komposisi – Media Masyarakat

Pengertian
👉 Fungsi/Pemetaan
Fungsi/Pemetaan yakni relasi dua himpunan A dan B yang memasangkan setiap anggota A dengan tepat satu anggota B.

dari gambar diatas kenapa gambar yang sebelah kanan termasuk bukan fungsi ? jawabannya sebab gambar seblah kanan ada anggota di himpunan A yang mempunyai 2 pasangan di himpunan B.

👀 Himpunan A disebut domain (tempat asal).

Cara penulisan domain: D = a,b,c

👀 Himpunan B disebut kodomain (kawasan mitra).

Cara penulisan kodomain: K = d,e,f

👀 Himpunan anggota B yang merupakan hasil pasangan dari himpunan A disebut range (daerah hasil).

Cara penulisan range: R = d,f

Sifat-sifat Fungsi
1. Fungsi Injektif (satu-satu)

Dua himpunan A dan B disebut fungsi injektif apabila setiap anggota B hanya memiliki satu pasangan dengan anggota himpunan A.
🙋 Adapun pola fungsi injektif:

👀 Gambar pertama merupakan fungsi injektif ,karena anggota himpunan B cuma memiliki satu pasangan pada himpunan A

👀 Gambar kedua merupakan fungsi injektif, alasannya adalah anggota himpunan B cuma mempunyai satu pasangan pada himpunan A walaupun ada satu anggota B yang tidak memiliki pasangan

👀 Gambar ketiga meupakan bukan fungsi injektif, karena ada anggota B yang memiliki dua pasangan pada himpunan A yakni (a2, b3) dan (a3, b3)

2. Fungsi Surjektif (onto)

Dua himpunan A dan B disebut fungsi surjektif apabila setiap anggota himpunan B merupakan pasangan dari anggota himpunan A. Dengan kata lain, anggota himpunan B merupakan kodomain sekaligus range. Adapun teladan fungsi surjektif:

👀 Gambar pertama merupakan fungsi surjektif, alasannya semua anggota himpunan B memiliki pasangan di himpunan A

👀 Gambar kedua merupakan bukan fungsi surjektif, alasannya ada anggota himpunan B yang tidak memiliki pasangan di himpuanan A yakni s

3. Fungsi Bijektif (korespondensi satu-satu)

Dua himpunan A dan B disebut fungsi bijektif apabila setiap anggota himpunan B mempunyai pasangan dari anggota himpunan A dan masing-masing anggotanya hanya mempunyai satu pasangan. Kaprikornus fungsi bijektif merupakan gabungan dari fungsi injektif dan surjektif.
🙋 Berikut contoh fungsi bijektif:

Gambar pertama merupakan fungsi bijektif, karena setiap anggota memiliki pasangan dan hanya mempunyai satu pasangan di himpunan A
Gambar kedua merupakan bukan fungsi bijektif, alasannya adalah ada anggota B yang memiliki dua pasangan di himpunan A yaitu (a,p) dan (b,p)

Latihan Fungsi Komposisi Dan Invers Fungsi

Jenis-jenis Fungsi
Secara garis beras fungsi fungsi terdiri dari fungsi aljabar dan fungsi transenden. Adapun yang akan kita diskusikan yakni jenis dari fungsi aljabar yaitu:
1. Fungsi Konstan (fungsi tetap)

Fungsi konstan yakni suatu fungsi yang memiliki nilai tetap/sama jika variabelnya disubstitusikan dengan nilai berapapun. Fungsi konstan dirumuskan f(x) = c, dengan c ialah konstanta. Grafik fungsi konstan berupa garis mendatar yang sejajar dengan sumbu x.

🙋 Contoh:
Diketahui rumus fungsi f(x) = 3 dengan kawasan domain -3,-2,-1,0,1. Gambarkan grafiknya!

Jawab:

2. Fungsi Linear

Fungsi linear ialah suatu fungi yang mempunyai grafik berupa garis lurus dengan rumus f(x) = ax + b dengan a tidak sama dengan 0.

🙋 Contoh:
DIketahui suatu fungsi f(x) = 2x + 3. Gambar grafiknya !
Jawab:

3. Fungsi Kuadrat

Fungsi kuadrat yakni suatu fungsi yang memiliki grafik berupa parabola, dengan rumus umum dari fungsi kuadrat $f(x)=ax^2+bx+c$ , dengan a tidak sama dengan nol.

🙋 Contoh

Fungsi f diputuskan oleh $f(x)=x^2+2x-3$ , gambar grafiknya selaku berikut.

Fungsi Komposisi
A. Definisi
Fungsi komposisi adalah penggabungan operasi dua fungsi secara berurutan sehingga menciptakan suatu fungsi gres. Operasi fungsi komposisi biasanya dilambangkan dengan “o” yang dibaca komposisi/ bundaran. Bentuk umum fungsi komposisi yakni sebagai berikut.
$(fog)(x)=f(g(x))$ atau $(gof)(x)=g(f(x))$

🙋  Contoh
Diketahui dua buah fungsi yakni,
$f(x)= 3x+2$
$g(x)= 2-x$

Tentukanlah
a. $(fog)(x)$
b. $(gof)(x)$

👉 Pembahasan
$f(x)= 3x+2$
$g(x)= 2-x$

a. ( fog )( x )
( fog )(x)=f (g(x))
= 3( 2 – x ) + 2
= 6 – 3x +2
= 8 – 3x

b. ( g o f) (x)
(g o f )(x)=g ( f(x))
= 2 – ( 3x + 2 )
= 2 – 3x – 2
= – 3x

B. Nilai Fungsi Komposisi
Nilai fungsi didapat dengan mensubstitusikan nilai x pada suatu fungsi. Untuk mengerti nilai fungsi komposisi, perhatian teladan berikut.

🙋  Contoh:
1. Diketahui $f(x)=5x^2+2$ dan $g(x)=x+1$ . Tentukan nilai $(fog)(-1)$ !

👉 Pembahasan
$(fog)(x)=f(g(x))$
$=f(x+1)$
                 $=5(x+1)^2+2$

$(fog)(-1)=5(-1+1)^2+2$

                     $=5(0)^2+2$

                     $=0+2=2$
🙋  Contoh:
Diketahui $f(x)=x+2$ dan $g(x)=3x$ . Tentukan nilai $(gof)(2)$ !

👉 Pembahasan
$(gof)(x)=g(f(x))$
                  $=g(x+2)$
                  $=3(x+2)$

$(gof)(2)=3(2+2)$
                 $=3(4)=12$

C. Sifat-sifat Komposisi Fungsi
1). Operasi komposisi pada fungsi-fungsi kebanyakan tidak bersifat komutatif

Latihan Fungsi Komposisi Dan Invers Fungsi

$(fog)(x)=\neq (gof)(x)$

2). Operasi komposisi pada fungsi-fungsi bersifat asosiatif

$(fo(goh))(x)=((fog)oh)(x)$

3). Dalam operasi komposisi pada fungsi-fungsi terdapat fungsi identitas, yaitu $f(x)=x$ sehingga berlaku

$(foI)(x)=(Iof)(x)=f(x)$

D. Menentukan Fungsi f kalau fungsi g dan gof atau fog Diketahui

🙋 Contoh
1. Tentukanlah g(x) jikalau f(x) = 2x + 4 dan $(gof)(x)=4x^2+12x+6$

👉 Pembahasan
$(gof)(x)=g(f(x))=4x^2+12x+6$

$g(2x+4)=4x^2+12x+6$
Misal $y=2x+4\rightarrow x=\fracy-42$ sehingga
$g(y)=4\left ( \fracy-42 \right )^2+12\left ( \fracy-42 \right )+6$

         $=4\left ( \fracy^2-8y+164 \right )+6(y-4)+6$

         $=y^2-8y+16+6y-24+6$

$g(y)=y^2-2y-2$
Kaprikornus, $g(x)=x^2-2x-2$

🙋  Contoh
2. Diketahui $g(x)=7x-5$ dan $(gof)(x)=2x^2+4x-5$ . Tentukan rumus f(x) !

👉 Pembahasan
$(gof)(x)=g(f(x))=2x^2+4x-5$

$7(f(x))-5=2x^2+4x-5$

$7(f(x))=2x^2+4x-5+5$

Jadi, $f(x)=\frac2x^2+4x7$

Itulah pembahasan singkat perihal fungsi dan fungsi komposisi, biar postingan ini berguna untuk teman-sobat semua. Untuk menambah pengetahuan kalian, kami menawarkan beberapa tipe soal yang berkaitan dengan fungsi komposisi.

Berikut soal dan pembahasannya, yuk kita simak !

Soal dan Pembahasan
1. Diketahui $f(x)=2x+5$ dan $g(x)=x^2+x-4$ . Nilai dari $f(5)-2(g(-4))=$ …

👉 Pembahasan
$f(x)=2x+5$
$f(5)=2(5)+5=10+5=15$

$g(x)=x^2+x-4$

$g(-4)=(-4)^2+(-4)-4=16-4-4=8$

$f(5)-2(g(-4))=15-2(8)=15-16=-1$

2. Jika $f(x)=3x-2$ dan $g(x)=x^2+1$ . Tentukan nilai $(fog)(x)+2((gof)(x))$ !

👉 Pembahasan
$(fog)(x)=f(g(x))$

                  $=3(x^2+1)-2$

                  $=3x^2+3-2=3x^2+1$

$(gof)(x)=g(f(x))$

                 $=(3x-2)^2+1$

                $=9x^2-12x+4+1$

                $=9x^2-12x+5$
Makara, $(fog)(x)+2((gof)(x))$

          $=3x^2+1+2(9x^2-12x+5)$

     $=3x^2+1+18x^2-24x+10$

         $=21x^2-24x+11$

3. Diketahui f(x) = – 2x + 3 dan $g(x)=x^2-4x+5$ . Komposisi fungsi (gof)(x) = …

👉 Pembahasan
$(gof)(x)=g(f(x))$
                   $=g(-2x+3)$
                   $=(-2x+3)^2-4(-2x+3)+5$
                  $=4x^2-12x+9+8x-12+5$
$(gof)(x)=4x^2-4x+2$

4. Jika $(fog)(x)=2x^2+4$ dan $f(x)=x-2$ maka g(x) = …

👉 Pembahasan
$(fog)(x)=2x^2+4$
$f(g(x))=2x^2+4$
$g(x)-2=2x^2+4$
$g(x)=2x^2+4+2$
$g(x)=2x^2+6$

5. Jika $(fog)(x)=2x+4$ dan $g(x)=x+1$ maka f(x) = …

👉 Pembahasan
$(fog)(x)=2x+4$
$f(g(x))=2x+4$

$f(x+1)=2x+4$
Misal $y=x+1\rightarrow x=y-1$ sehingga
$f(y)=2(y-1)+4$
$f(y)=2y-2+4$
Kaprikornus,

$f(x)=2x+2$

Untuk Latihan Online Silahkan Klik di SINI