Fungsi invers dari fungsi komposisi merupakan materi lanjutan dari fungsi invers matematika dan fungsi komposisi, jadi kedua materi tersebut adalah materi prasyarat untuk mempelajari materi ini. . Jika anda belum menguasai kedua materi diatas pelajari terlebih dahulu pada bagian lain dari blog ini.
Jika h(x) adalah fungsi komposisi yang dibentuk dari fungsi f(x) dan g(x), maka kemungkinan fungsi h(x) adalah :
sehingga fungsi invers dari h (x) adalah :
Bentuk-bentuk seperti ^{-1}(x)\,&space;atau\,&space;(g\circ&space;f)^{-1}(x)) seperti ini disebut fungsi invers dari fungsi komposisi.
seperti ini disebut fungsi invers dari fungsi komposisi.
Bagaimana cara menentukan fungsi invers dari fungsi komposisi? Dibawah ini rumus fungsi invers dari fungsi komposisi adalah :
Agar lebih memahami cara menentukan fungsi invers dari fungsi komposisi, perhatikan contoh-contoh dibawah ini :
Contoh 1 :
[Penyelesaian]
(x)=g\left&space;(&space;f(x)&space;\right&space;)=g(2x-1)&space;\\(g\circ&space;f)(x)=1-(2x-1)=-2x+1&space;\\\\\Leftrightarrow&space;Misalkan\,&space;y=(g\circ&space;f)(x)=-2x+1&space;\\\Leftrightarrow&space;y=-2x+2&space;\\\Leftrightarrow&space;2x=-y+2)
&space;\\\Leftrightarrow&space;f^{-1}(y)=\frac{1}{2}(-y+2)&space;\\\Leftrightarrow&space;(g\circ&space;f)^{-}(y)=\frac{1}{2}(-y+2))
^{-1}(x)=\frac{1}{2}(-x+2)})
sekarang kita tentukan (x)) , yaitu:
, yaitu:
=2x-1\,&space;\,&space;maka\,\,&space;f^{-1}(x)=\frac{1}{2}(x+1)&space;\\\Leftrightarrow&space;misalkan,&space;\,&space;g(x)=1-x\,&space;\,&space;maka\,\,&space;g^{-1}(x)=(1-x))
Maka,
Contoh 2:
Diketahui fungsi f dan g sebagai berikut :
Tentukanlah :
\,&space;\left&space;(&space;f\circ&space;g&space;\right&space;)^{-1}\left&space;(&space;x&space;\right&space;)\\\\&space;(b)\left&space;(&space;g\circ&space;f&space;\right&space;)^{-1}\left&space;(&space;x&space;\right&space;))
[Penyelesaian]
=\frac{9}{x+3}\rightarrow&space;\,&space;f^{-1}\left&space;(&space;x&space;\right&space;)=\frac{-3x+9}{x})
=x^{2}\rightarrow&space;g^{-1}\left&space;(&space;x&space;\right&space;)=\sqrt{x})
Daftar Isi
Fungsi invers dari fungsi komposisi – Cara cepat menentukan fungsi invers , dengan rumus khusus:
Rumus diatas dapat digunakan untuk mencari fungsi invers dari fungsi komposisi, pada soal dibawah ini :
Contoh 3:
Diketahui =(g\circ&space;f)(x)) , tentukanlah
, tentukanlah ) jika diketahui :
jika diketahui :
=\frac{1}{x-1}\:,\,&space;dan\:&space;\:&space;g^{-1}(x)=\frac{1-x}{x})
.[Penyelesaian]
Gunakan rumus (2), untuk mencari ) :
:
Coba variasi soal yang lain dari menentukan fungsi invers dari fungsi komposisi , berikut ini :
Contoh 4:
Tentukan nilai f (2)jika, diketahui :
[Penyelesaian]
Transformasi komposisi matriks
Pada transformasi linear khususnya matriks juga berlaku fungsi komposisi yang disebut transformasi komposisi. Berikut rumus menentukan fungsi invers dari fungsi komposisi tersebut,
Jika matriks transformasi linear f dan g berturut-turut dan B
Maka matriks f ○ g = A x B , dan matriks g ○ f = B x A
Silahkan simak contoh-contoh soal tentang fungsi invers dari fungsi komposisi yang berhubungan dengan matriks dibawah ini.
Contoh 5 :
Diketahui matriks transformasi linear f dan g berturut-turut, 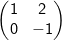 dan
dan 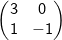
Tentukanlah matriks transformasi komposisi :
(a) f ○ g (b) g ○ f
[Penyelesaian]
Materi prasyarat yang harus dikuasai terlebih dahulu untuk mengerjakan soal ini adalah matriks dan perkalian matriks
Materi prasyarat yang harus dikuasai terlebih dahulu untuk mengerjakan soal ini adalah matriks dan perkalian matriks
(a) =\begin{pmatrix}&space;3&space;&&space;0\\&space;1&&space;-1&space;\end{pmatrix}\begin{pmatrix}&space;1&space;&&space;2\\&space;0&space;&&space;-1&space;\end{pmatrix}=\mathbf{\begin{pmatrix}&space;3&space;&6&space;\\&space;1&&space;3&space;\end{pmatrix}})
(b)=\begin{pmatrix}&space;1&space;&&space;2\\&space;0&&space;-1&space;\end{pmatrix}\begin{pmatrix}&space;3&space;&&space;0\\&space;1&space;&&space;-1&space;\end{pmatrix}=\begin{pmatrix}&space;5&space;&-2&space;\\&space;-1&&space;1&space;\end{pmatrix})
Contoh 6 :
Diketahui matriks transformasi linier f dan g , yaitu 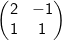 dan
dan 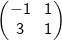 tentukanlah
tentukanlah ^{-1})
[Penyelesaian]
Materi prasyarat yang harus di kuasai sebelumnya untuk mengerjakan soal ini adalah invers matriks dan determinan matriks.
Tentukan terlebih dahulu) yaitu,
yaitu,
=\begin{pmatrix}&space;-1&space;&&space;1\\3&space;&1&space;\end{pmatrix}\begin{pmatrix}&space;2&space;&&space;-1\\&space;1&space;&&space;1&space;\end{pmatrix}=\begin{pmatrix}&space;-1&&space;2\\&space;7&&space;-2&space;\end{pmatrix})
Materi prasyarat yang harus di kuasai sebelumnya untuk mengerjakan soal ini adalah invers matriks dan determinan matriks.
Tentukan terlebih dahulu
Maka
Penguasaan materi yang lain yang berhubungan dengan fungsi sangat membantu dalam memahami seperti fungsi irasional, fungsi kuadrat, fungsi rasional . Materi-materi tersebut juga sangat menunjang untuk mempelajari lebih jauh tentang fungsi invers dari fungsi komposisi.
Materi Terkait:
