Yap..
Mari kita kerjakan soal dengan model mirip ini..
Hati-hati ya, jangan hingga terkecoh. Jika tidak cermat, kita bisa salah mengkalkulasikan luas tumpukan kedua kubus ini.
Soal :
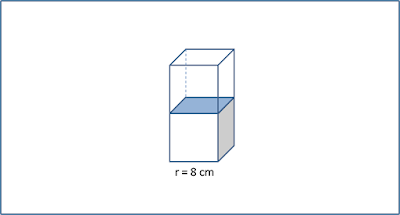
1. Dua buah kubus dengan rusuk 8 cm ditumpuk menjadi satu. Berapakah luas dan volume totalnya kini?
Kita mesti mencari dua hal :
- luas
- dan volume.
Perhatikan gambar dibawah ini..
Kubus dengan panjang rusuk 8 cm ditumpuk dan sekarang kita mampu mencari luas totalnya, luas tumpukan kubus yang baru ini.
Menjadi apakah kubus ini sekarang?
Balok..
Kita bisa memanfaakan rumus luas balok untuk mendapatkan luas permukaan dua tumpukan kubus ini.
Masih ingat dengan rumus luas balok?
Luas balok = 2(pl + pt + lt)
Diketahui :
- p = 8 cm
- l = 8 cm
- t = 16 cm
Volume total ialah volume kubus bawah ditambah dengan volume kubus atas.
Volume total = Volume kubus + volume kubus
Volume total = V + V
- Kedua kubus ukurannya sama, jadi volumenya juga sama.
- V = r³
- r = 8 cm
2. Dua buah kubus dengan rusuk 4 cm ditumpuk menjadi satu. Berapakah luas dan volume totalnya sekarang?
Cara dan langkahnya sama dengan soal pertama..
Dua kubus yang ditumpuk akan menjadi balok dan yang berganti hanyalah tingginya saja. Tinggi balok ialah dua kali rusuk kubus.
Tinggi (t) = 2r
t = 2.4
t = 8 cm
Diketahui :
- p = 4 cm
- l = 4 cm
- t = 8 cm
- r = 4 cm