Artikel kali ini akan membicarakan tentang bangun ruang bola. Pada bahan bangun datar, kalian telah mempelajari perihal berdiri lingkaran.
Apa saja bagian-komponen yang terdapat dalam lingkaran?
Apakah kalian masih mengingatnya?
Salah satu unsur dalam bulat yakni jari-jari. Nah, pada peluang kali ini kita akan membicarakan tentang salah satu berdiri ruang yang juga memiliki komponen jari-jari.
Bangun ruang apakah itu? Simak penjelasan di bawah ini.
Daftar Isi
Definisi Bola
Perhatikan gambar berikut.
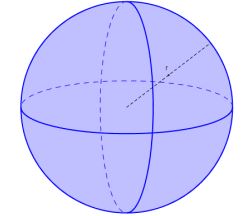
Salah satu berdiri ruang yang unsurnya merupakan jari-jari yakni bangkit ruang bola.
Apa itu berdiri ruang bola?
Bola merupakan salah satu bangun ruang sisi lengkung yang tersusun dari tak terhingga banyaknya lingkaran yang berpusat di satu titik ialah titik sentra bola.
Bola juga dapat diartikan selaku himpunan semua titik dalam dimensi tiga yang berjarak sama dengan sebuah titik teladan, yaitu titik sentra bola.
Selanjutnya, amati beberapa contoh penerapan bola dalam kehidupan sehari-hari.
Bola dalam Kehidupan Sehari-hari
Terdapat banyak contoh penerapan bola dalam kehidupan sehari-hari.
Beberapa objek yang berbentuk mirip bola mirip bola basket, bola kasti, kelereng, dan objek yang mirip bulat lainnya.
Selanjutnya akan dijelaskan perihal sifat-sifat bola.
Sifat-Sifat Bola
Perhatikan gambar bangkit bola di bawah ini.

Pada gambar tersebut terdapat beberapa ciri-ciri atau karakteristik yang membedakan antara bangun ruang bola dengan berdiri-bangkit ruang lainnya.
Apa sajakah karakteristik tersebut?
Berikut ialah karakteristik bangkit ruang bola.
- Bangun ruang bola mempunyai satu segi. Sisi bola ialah kumpulan titik-titik yang berjarak sama dengan sentra bola. Sisi bola tersebut mampu disebut sebagai permukaan bola atau selimut bola.
- Bangun ruang bola tidak mempunyai rusuk.
- Pada gambar di atas, bagian yang diberi nama dengan r ialah jari-jari bola. Jari-jari bola menghubungkan titik pusat bola dengan titik pada permukaan bola.
- Sama dengan bahan pada bangun bulat, diameter bola ukurannya dua kali ukuran jari-jari bola.
- Ruang garis yang menghubungkan dua titik pada bola disebut dengan tali busur bola. Tali busur bola terpanjang merupakan diameter bola.
Rumus Bola
Berikut akan diterangkan beberapa rumus yang dipakai dalam materi bangkit ruang bola. Rumus yang hendak kita bahas pada bab ini adalah rumus luas permukaan bola dan rumus volume bola.
Perhatikan gambar berikut.
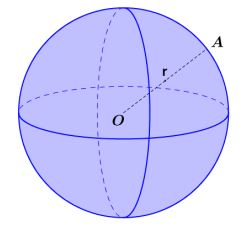
Pada gambar di atas, jari-jari bola ditunjukkan oleh ruas garis OA dan titik sentra bola ditunjukkan oleh titik O. Titik A terletak pada permukaan bola.
Rumus Luas Permukaan Bola
Rumus luas permukaan bola mampu dituliskan selaku berikut.
Lp = 4 x π x r2
Keterangan:
Lp : Luas permukaan bola
r : jari-jari bola
π : konstanta yang bernilai 3,14159 . . .
Selanjutnya akan diterangkan tentang volume bola.
Rumus Volume Bola
Volume bola dirumuskan selaku :
V = (4/3) x π x r3
Keterangan:
V : Volume bola
r : jari-jari bola
π : konstanta yang bernilai 3,14159 . . .
Coba lakukan soal berikut untuk mengembangkan pengertian kalian tentang bangun ruang bola.
Contoh Soal Bola
1. Terdapat sebuah bola dengan jari-jari 21 cm. Tentukan luas permukaan dan volume bola tersebur. (Gunakan π = 22/7).
Diketahui: r = 21 cm.
Lp = 4 x π x r2 = 4 x (22/7) x 21 cm x 21 cm = 5.544 cm2
V = (4/3) x π x r3 = (4/3) x (22/7) x 21 cm x 21 cm x 21 cm = 38.808 cm3.
2. Terdapat dua buah bola dengan jari-jari bola masing-masing ialah 4 cm dan 12 cm. Tentukan perbandingan volume dua bola tersebut.
V = (4/3) x π x r3
Diketahui: r = 4 cm dan R = 12 cm.
Vkecil/Vbesar = ((4/3) x π x r3)/( (4/3) x π x R3) = r3/R3 = (4 x 4 x 4)/(12 x 12 x 12) = 1/27.
Perbandingan volume dua bola tersebut ialah 1 : 27.
Mari kita simpulkan bareng .
Kesimpulan
- Bola merupakan salah satu bangun ruang segi lengkung yang tersusun dari tak terhingga banyaknya bundar yang berpusat di satu titik adalah titik pusat bola. Bola juga dapat diartikan selaku himpunan semua titik dalam dimensi tiga yang berjarak sama dengan suatu titik pola, yakni titik pusat bola.
- Rumus luas permukaan bola ialah Lp = 4 x π x r2.
- Rumus volume bola yakni V = (4/3) x π x r3.
Demikian pembahasan tentang bangkit ruang bola. Semoga mampu menawarkan banyak faedah bagi pembaca semuanya.