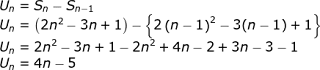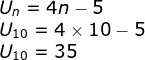Daftar Isi
Barisan dan Deret Aritmetika dan Geometri
Barisan dan Deret aritmatika sma
Barisan dan deret aritmatika Sekolah Menengan Atas maupun Sekolah Menengah kejuruan ialah materi lanjutan dari barisan dan deret matematika SMP, paling tidak materi tersebut sedikit banyak telah kalian pelajari.
Barisan Aritmatika
Barisan aritmatika ialah suatu barisan yang memiliki selisih dua suku yang berurutan (beda) selalu tetap.Bentuk lazimnya ialah:
a, (a + b), (a + 2b), …, a + (n – 1) b
Keterangan:
a = U1 = suku pertama
b = beda = 
Un = suku ke-n
n = banyaknya suku
Rumus Suku ke-n Barisan Aritmatika
Rumus suku ke-n dari barisan aritmatika adalah:( rumus-suku-ke-n-barisan- aritmatika)
Contoh Soal dan Pembahasan Barisan Aritmatika
1.Tentukanlah suku pertama, beda, dan suku ke-10 dari barisan aritmatika 8 , 4 , 0, – 4, – 8, …
[Penyelesaian]
a = 8 ; b = – 4 dan
.(-4)&space;\\U_10=8-36&space;\\U_10=-28 "Barisan dan Deret")
2. Tentukan suku pertama dan beda dari barisan aritmatika yang suku ke-7 nya yakni 11 dan suku ke-20 nya ialah – 41.
[Penyelesaian]
.b=11&space;\\&space;a+6b=11\,&space;\,&space;.....(1)&space;\\U_20=a+(20-1)b=-41&space;\\a+19b&space;=-41\,&space;.....(2) "Barisan dan Deret")
Dari (2) – (1) , diperoleh a = 35 dan d = – 4
3.Tentukanlah lima bilangan yang bila disisipkan diantara 7 dan 25 akan menjadi barisan aritmatika
[Penyelesaian]
Karena a = 7 dan  "Barisan dan Deret")
Subtitusikan a = 7 ke (1), diperoleh b = 3, maka kelima bilangan tersebut adalah 7, 10, 13 , 16, 19, 22
4.Suatu segitiga siku-siku ketiga sisinya membentuk barisan aritmatika, tentukanlah perbandingan ketiga sisi segitiga tersebut.
[Penyelesaian]
Misalkan beda ketiga segi segitiga tersebut yakni b maka barisan tersebut yaitu a – b, a dan a + b.
Karena ketiga sisinya membentuk tripel phytagoras maka:
^2=&space;a^2&space;+&space;(a-b)^2&space;\\a^2+2ab+b^2=&space;a^2+a^2-2ab+b^2&space;\\a^2-4ab=0&space;\\a(a-4b)=0&space;\\a-4b=0&space;\\a=4b "Barisan dan Deret")
karena a = 4b maka segi-sisi ketiga segitiga tersebut yaitu 3b, 4b dan 5b, maka perbandingan ketiga sisinya yaitu:
3b : 4b : 5b = 3 : 4 : 5
Suku tengah barisan Aritmatika
Jika suatu barisan aritmatika memiliki suku ganjil maka suku tengahnya ialah:
Sisipan pada Barisan Aritmatika
Jika diantara dua buah suku berurutan pada barisan aritmatika disisipkan k buah suku, maka akan didapat barisan aritmatika gres dengan hubungan sebagai berikut:
Barisan aritmatika usang : a, (a + b)
Barisan aritmatika gres : a, (a + b’), (a + 2b’), . . ., (a + b)
k yakni suku baru yang disisipkan , maka hubungan barisan aritmatika yang usang dengan yang gres yaitu:
Keterangan:
b’ = beda barisan aritmatika gres
b = beda barisan aritmatika usang
k = banyak suku yang disisipkan
n = banyak suku barisan aritmatika lama
n’ = banyak barisan aritmatika baru
Yang perlu diingat dalam sisipan adalah: a = a’ , Un = Un dan Ut = Ut
Contoh Soal:
Diketahui barisan aritmatika 2, 5, 8, 11, 14 Diantara setiap dua suku di sisipkan 5 buah suku baru .Tentukanlah beda, banyak suku dan suku ke- 20 dari barisan aritmatika yang baru!
[Penyelesaian]
b = 3 ; dan 
k = 5 dan n’ = n + (n –1)k = 5 + (5 – 1).5 = 25
dan suku ke-20 adalah: 
Deret Aritmatika (Deret Hitung)
Deret aritmatika ialah jumlah dari suku-suku barisan aritmatika, rumus jumlah parsial dari n suku barisaannya adalah:
Keterangan:
Sn = Jumlah n suku pertama
n = banyak suku
Un = Suku ke-n
b = beda
Hubungan antara Sn, S_(n-1), dan Un ialah:
Un = suku ke-n
Sn= Jumlah n suku pertama
Contoh Soal:
Diketahui deret aritmatika 
.Tentukan 
[Penyelesaian]
Maka rumus Un yaitu :
Kaprikornus U10 yaitu:
Hubungan antara Suku tengah (Ut) dan Sn
Jika banyaknya suku barisan aritmatika ganjil yakni n, a suku pertama dan Un suku terakhir maka korelasi antara suku tengah dan jumlah deret aritmatika Sn adalah:
Barisan dan Deret Aritmatika Contoh Soal dan Pembahasan
1.Diketahui deret aritmatika dengan suku ke-n yakni Un dan jumlah n suku pertama yakni Sn. Jika 
dan 
Tentukanlah 
.
[Penyelesaian]
Soal ini saya ambil dari soal SNMPTN UNPAR Bandung, ihwal barisan dan deret aritmatika.
^2+(a+2b)^2&space;\\a^2=a^2+2ab+b^2+a^2+4ab+b^2&space;\\a^2+6ab+5b^2=0&space;\\(a+5b)(a+b)=0 "Barisan dan Deret")
a= – 5b karena a = 20 , maka b = – 4, jadi
&space;\\\\S_3=3(a+b)=&space;3(16)=\mathbf48 "Barisan dan Deret")
2.Diketahui barisan aritmatika 2, 9, 16, 23, …. Tentukan jumlah semua suku yang nilainya kurang dari 100.
[Penyelesaian]
Tentukan dahulu rumus suku ke-n:
.7&space;\\U_n=7n-5 "Barisan dan Deret")
Karena jumlah semua suku yang ditanya kurang dari 100, maka
Makara jumalah suku yang nilainya kurang dari 100 yakni:
2&space;\\\\S_14=\mathbf665 "Barisan dan Deret")
turunan fungsi 
, maka:
3.Jumlah n suku pertama deret aritmatika yakni  "Barisan dan Deret")
tentukanlah rumus suku ke-n barisan ini!
[Penyelesaian]
&space;\\\\S_n=\frac72n^2+\frac112n "Barisan dan Deret")
Cara cepat mencari 
:
Soal tantangan perihal Barisan Aritmatika dan Geometri
Ini ada soal tantangan, mungkin tantangan atau bagi yang lain ini soal mudah tergantung deh..he.he! Tapi sebelumnya saya mau share rumus rata-rata aritmatika dan rumus rata-rata geometri sekalian deh sama rumus rata-rata serasi dari tiga bilangan sesuai urutan a , x dan b.
1. Rumus rata- rata aritmatika tiga bilangan sesuai urutan a, x , b
2. Rumus rata- rata geometri tiga bilangan sesuai urutan a, x ,b
3. Rumus rata- rata harmonis tiga bilangan sesuai urutan a, x , b
2. Rumus rata- rata geometri tiga bilangan sesuai urutan a, x ,b
3. Rumus rata- rata harmonis tiga bilangan sesuai urutan a, x , b
Rumusnya udah kan.., kini pribadi ke contoh soalnya aja!
Tiga buah bilangan sesuai dengan urutan 8, a dan b membentuk barisan aritmatika sedangkan a,b dan 36 sesuai urutannya membentuk barisan geometri.Tentukanlah nila a dan b
[Penyelesaian]
alasannya adalah a yakni rata-rata aritmatika dari 8 dan b, maka:
karena b yaitu rata-rata geometri dari a dan 36, maka:
….(2)
Subtitusikan (1) ke (2), langsung aja ya dapetnya segini:
Demikian pembahasan bahan barisan dan deret aritmatika, aku akan update terus soal-soal dalam postingan ini. Kritik dan usulan sampaikan pada kolom komentar, supaya berguna!