Di dalam soal cuma diketahui panjang sisi miring sebuah segitiga siku-siku dan kita diharuskan mencari luasnya..
Teori pitagoras sungguh menolong..
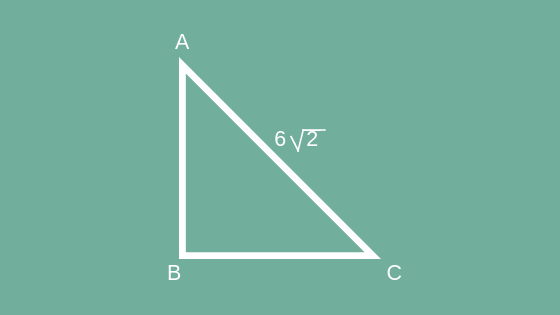
1. Sebuah segitiga siku-siku sama kaki mempunyai panjang sisi miring 6√2 cm. Berapakah luas segitiga itu?
Gambar segitiganya mampu dilihat seperti dibawah.
Karena segitiga siku-siku sama kaki, maka panjang kaki-kakinya pastilah sama.
Sehingga :
- AB = BC
Misalkan AB dan BC selaku “x”.
Menggunakan pemberian teori pitagoras, kita mampu memperoleh nilai x. Tinggal masukkan nilai yang dikenali ke rumus dan hitung.
Rumus pitagoras :
AC² = AB² + BC²
Diketahui dari soal :
- AC = 6√2
- AB = x
- BC = x
- (6√2)² = 6√2 × 6√2
= 36×√4
= 36×2
= 72 - x² + x² =
= 2x²
72 = 2x²
- untuk mendapatkan x², bagi 72 dengan 2
- untuk mendapatkan x, akarkan 36
- AB = x = 6 cm
- AC = x = 6 cm
Alas dan tinggi dari segitiga sudah dikenali dan kita mampu mengkalkulasikan luasnya dengan memasukkan data ke dalam rumus luas.
- Alas = BC = 6cm
- tinggi = AB = 6 cm
2. Sisi miring sebuah segitiga siku-siku sama kaki panjangya 14√2 cm. Berapakah luas segitiga tersebut?
Caranya masih sama dengan soal pertama.
Karena dikenali sisi miring, maka dua sisi yang belum dimengerti adalah sisi tegaknya, yaitu bantalan dan tinggi.
- Karena siku-siku sama kaki, maka bantalan dan tingginya sama dan kita misalkan “n”
- Permisalan bebas, mau pakai x, n, m, p atau q, bisa kok..
Diketahui dari soal :
- AC = sisi miring = 14√2
- AB = tinggi = n
- BC = alas = n
- (14√2)² = 14√2 × 14√2
= 196×√4
= 196×2
= 392 - n² + n² =
= 2n²
392 = 2n²
- untuk mendapatkan n², bagi 392 dengan 2
- akarkan 196
- AB = n = 14 cm
- BC = n = 14 cm