Persamaan Kuadrat – Media Masyarakat

Daftar Isi

Persamaan Kuadrat SMA kelas X

http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html

Persamaan kuadrat adalah persamaan dalam peubah x , dengan peubah x paling tinggi berpangkat dua atau berderajat dua. Perhatikan beberapa contoh persamaan kuadrat dibawah ini:

Mencari Faktor 2x2 + 9x - 5 = 0

$\\(1).\, x^2-25=0\\(2). \, x^2-2x-15\\(3).\, 2x^2-5x+2=0$

Persamaan Kuadrat Matematika Bentuk Umum

Bentuk umum persamaan kuadrat adalah,

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$

Dari bentuk umum diatas, dapat kita gunakan untuk menentukan nilai a, b, dan c pada soal persamaan kuadrat dibawah ini.

$\\a.\, x^2-x+5=0, \Rightarrow a=1;b=-1;c=5\\\\b.\, 2x^2+2x=0\Rightarrow a=2;b=2;c=0\\\\c. \, -x^2+9=0\Rightarrow a=-1;b=0;c=9$

Menyelesaikan Dan Mencari Akar-akar Persamaan Kuadrat

Persamaan kuadrat dapat dicari akar-akarnya dengan tiga cara yaitu:

Memfaktorkan

Melengkapkan kuadrat sempurna

Dengan rumus abc

a. Menyelesaikan Persamaan Kuadrat dengan Memfaktorkan

Berdasarkan sifat perkalian dua faktor bilangan dengan hasil sama dengan 0,

pq = 0 ⇒ p = 0 atau q = 0

Contoh soal :

Tentukanlah penyelesaian dari persamaan kuadrat berikut ini dengan memfaktorkan!

1. Bentuk pemfaktoran 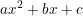$ax^2+bx+c$

yaitu
$x^2+4x-21=0$

[Penyelesaian]

$\\x^2+4x-21=0\\\ \(x-3)(x+7)=0\\\\x=3\, atau\, x=-7$

Jadi, Himpunan penyelesaian = {3,-7}

2. Bentuk pemfaktoran selisih kuadrat , ${\color{Green} \\a^2-b^2}{\color{Green} =}\, {\color{Green} (a+b)(a-b)}$ yaitu
$\small -5x^2+20=0$

[Penyelesaian]

$\\-5x^2+20=0\\\\x^2 -4=0\Leftrightarrow (x+2)(x-2)=0 \\\\x=2\, atau\, x=-2$

Jadi, Himpunan penyelesaian = {2,-2}

3. Bentuk pemfaktoran, ${\color {Green} ax^2\, \pm \, bx=ax(x+b)}{\color{Green} =0}$ yaitu
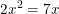
$\small 2x^2=7x$

[Penyelesaian]

$\\2x^2=7x\\\\2x^2-7x=0\\ \\x(2x-7)=0\\\\x=0\, atau\, x=\frac{7}{2}$
$=\left \{ 0,\frac{7}{2} \right \}$

a. Menyelesaikan Persamaan Kuadrat dengan melengkapkan kuadrat sempurna

Langkah-langkah melengkapkan kuadrat sempurna adalah :
Syaratnya koefisien $\small x^2=1$
Ubah bentuk persamaan kuadrat menjadi $\small x^2+bx=c$
Tambahkan ruas kiri dan ruas kanan dengan kuadrat dari setengah koefisien x nya atau $\small \left ( \frac{b}{2} \right )^{2}$
Tentukan akar-akar persamaan kuadrat tersebut

Contoh soal :

Tentukanlah Himpunan penyelesaian dari persamaan kuadrat berikut ini dengan melengkapkan kuadrat sempurna.

1. Ini adalah contoh jika koefisien $x^2=1$ yaitu
$\\x^2-6x-3=0\\x^2-6x=3\ \x^2-6x+(3)^2=3+(3)^2\\(x-3)^2=12\\x-3=\pm\sqrt{12}\Leftrightarrow x-3= \pm 2\sqrt{3}\\x=3\pm2\sqrt{3}$

2. Contoh kedua ini jika koefisien $\dpi {100} \small x^2\neq1$

yaitu,
$3x^2- 5x-8=0$

Koefisien 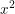$x^2$ dibuat sama dengan 1, dengan membagi 3 kedua ruas persamaan,

$\\3x^2-5x-8=0\\\ \x^2-\frac{5}{3}x-\frac{8}{3}=0\\\\x^2-\frac{5}{3}x=\frac{8}{3}$
$\\x^2-\frac{5} {3}x+\left ( \frac{5}{6} \right )^{2}=\frac{8}{3}+\left ( \frac{5}{6} \right )^{2}\\\\\left ( x-\frac{5}{6} \right )^{2}=\frac{121}{36}\Leftrightarrow x-\frac{5}{6}=\pm\frac{11}{6}\\\\x=\frac {5\pm11}{6}\Leftrightarrow x=\frac{4}{3}\, atau\, x=-1$

c. Menyelesaikan Persamaan Kuadrat dengan Rumus kuadrat atau rumus abc

Dibawah ini adalah pembuktian rumus kuadrat atau rumus abc dengan melengkapkan kuadrat sempurna:

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$
$\\\left ( x+\frac{b}{2a} \right )^{2}=\frac{b^2-4ac}{4a^2}\\\\x+\frac{b}{2a}=\pm\frac{\sqrt{b^2-4ac}}{2a}\\\\x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

maka rumus kuadrat dari 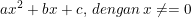$ax^2+bx+c,\, dengan\, x\neq=0$ dengan a≠ 0 adalah :

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$

Rumus ini lebih dikenal dengan nama rumus abc.

Contoh soal:

Tentukanlah Himpunan penyelesaian dari persamaan kuadrat berikut ini dengan menggunakan rumus kuadrat atau rumus abc.

1. Contoh soal persamaan kuadrat yang memiliki akar-akar real,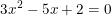 $3x^2-5x+2=0$

[Penyelesaiann]

Diketahui a = 3 ; b = -5 dan c = 2

$\\x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\\\=\frac{5\pm\sqrt{(-5)^2-4\times 3\times 2}}{2\times 3}\\\\=\frac{5\pm\sqrt{25-24}}{6}=\frac{5\pm1}{6}$
$\therefore x_{1}=1\, \, atau\, \, x_{2}=\frac{2}{3}$

2.Contoh persamaan kuadrat yang tidak mempunyai akar real (definit negatif ) atau akar-akarnya imajiner sering disebut juga mempunyai dua solusi kompleks berbeda,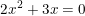 $2x^2+3x=0$ .

[Penyelesaian]

Diketahui a = 2 ; b = 0 dan c = 3

$\\=\frac{0\pm\sqrt{0^2-4\times2\times 3}}{2\times 2}\\\\=\frac{0\pm\sqrt{-24}}{4}=\frac{\pm2\sqrt{6}\, i}{4}=\frac{\pm\sqrt{6}\, i}{2}$

Hubungan Antara Jenis Akar dan Diskriminan Persamaan Kuadrat

Rumus diskriminan persamaan kuadrat adalah :

$D=b^2-4ac$

Dari nilai diskriminannya akar-akar suatu persamaan kuadrat dapat dikelompokkan seperti dibawah ini (Tampomas, 1999)

D > 0 , ⇒ Persamaan kuadrat tersebut mempunyai dua akar real berbeda

D < 0, ⇒ Persamaan kuadrat tersebut mempunyai dua akar kompleks berbeda atau tidak mempunyai akar-akar real

D = 0, ⇒ Persamaan kuadrat tersebut mempunyai dua akar yang sama atau kembar

Sifat Jumlah dan Hasil Kali Akar-akar Persamaan kuadrat

Misalkan diketahui 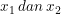$x_{1}\, dan\, x_{2}$ adalah akar-akar dari persamaan 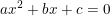$ax^2+bx+c=0$ , maka diperoleh :

a. Jumlah akar – akar persamaan kuadrat :

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$

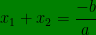
b. Hasil kali akar-akar persamaan kuadrat :

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$

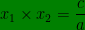
c. Selisih persamaan kuadrat x1-x2 :

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$

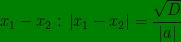
Hubungan Antara Koefisien Dan Sifat-sifat Akar Persamaan Kuadrat

(a). Persamaan kuadrat kedua akarnya berlawanan

$x_{1}=-x_{2}\Rightarrow b=0$

(b). Persamaan kuadrat yang kedua akarnya berkebalikan

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$

(c). Persamaan kuadrat yang akarnya kembar atau sama

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$

(d). Persamaan kuadrat salah satu akarnya = 0

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$

Menyusun Persamaan Kuadrat Baru

a. Menyusun Persamaan Kuadrat Jika Akar-akarnya Diketahui

Dengan cara memakai faktor

Diketahui 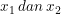$\small x_{1}\, dan\, x_{2}$ akar-akar dari persamaan kuadrat $ax^2+bx+c=0\Rightarrow (x-x_{1})(x-x_{2})=0$

Dengan Rumus jumlah dan hasil kali akar-akarnya

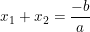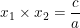DiketahuiQ $x_{1}+x_{2}=\frac{-b}{a}$ dan $x_{1}\times x_{2}=\frac{c}{a}$ , maka persamaan kuadratnya ,

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$

Maka rumus persamaan kuadrat jika diketahui jumlah dan hasil kali akar-akarnya adalah:

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$

b.Menyusun Persamaan kuadrat baru yang akar-akarnya berkebalikan

Jika 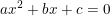$ax^2+bx+c=0$ akar-akarnya α ( alfa ) dan β ( Beta ) persamaan kuadrat yang baru dari 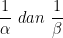$\frac{1}{\alpha}\,\, dan\,\, \frac{1}{\beta }$ adalah :

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$

c. Menyusun Persamaan kuadrat baru yang akar-akarnya 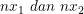$nx_{1}\, \, dan\, \, nx_{2}$

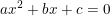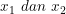Jika $\small ax^2+bx+c=0$ akar-akarnya $x_{1}\, \, dan\, \, x_{2}$ , persamaan kuadrat yang baru yang akar-akarnya 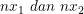$nx_{1}\, \, dan\, \, nx_{2}$ adalah:

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$

d. Menyusun Persamaan kuadrat baru yang akar-akarnya $(x_{1})^{2}\, \, dan\, \, (x_{2})^{2}$

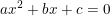Jika $\small ax^2+bx+c=0$ akar-akarnya x1 dan x2, persamaan kuadrat yang baru yang akar-akarnya $(x_{1})^{2}\, \, dan\, \, (x_{2})^{2}$ adalah:

$a^2x^2-(b^2-2ac)x+c^2=0$

e. Menyusun Persamaan kuadrat baru yang akar-akarnya 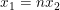$\small x_{1}=nx_{2}$

Jika 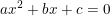$\small ax^2+bx+c=0$ akar-akarnya x1 dan x2, persamaan kuadrat yang baru yang akar-akarnya 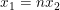$x_{1}=nx_{2}$ adalah:

$http://soulmath4u.blogspot.com/2014/01/persamaan-kuadrat.html$

Soal – soal persamaan kuadrat kelas 10 dalam kehidupan sehari-hari dan penyelesaiannya

Dibawah ini contoh soal persamaan kuadrat dalam kehidupan sehari-hari dan sering muncul

pada Ujian Nasional (UN) SMA maupun SNMPTN .

1.Dalam sebuah ruangan kelas yang berbentuk persegi panjang mempunyai kapasitas tempat

duduk sebanyak 72 kursi. Jika kursi-kursi diatur kembali dengan cara menambahkan 3 buah

kursi lagi pada setiap barisnya, maka jumlah baris akan berkurang 2 baris. Hitunglah berapa banyak jumlah kursi pada setiap baris mula-mula!

[Penyelesaian]

Kapasitas kursi dalam ruangan = 72 kursi

Misalkan jumlah kursi pada setiap baris mula-mula = x

Dan jumlah baris mula-mula = y

Maka,
$\\xy=72\, \, ....\, (1)\\(x+3)(y-2)=72\, \, ....\, (2)$

Dari (2):

xy-2x+3y-6=72

72-2x+3y-6=72

-2x+3y=6

3y = 2x+6 ………..(3)

Dari (1)× 3 :

x× 3y = 216

x(2x+6)=216

$\\2x^2+6x-216=0\\x^2+3x-108=0\\(x-9)(x+12)=0\\x=9\: ;\: x=-12\, (tidak \, memenuhi)$

Jadi, jumlah kursi pada setiap baris mula-mula adalah 9 buah.

2.Sebuah proyek pengerjaan taman rumah biayanya Rp 2000.000;00 dibagikan sama rata kepada setiap pekerjanya. Jika dua orang pekerja mengundurkan diri maka setiap pekerja akan menerima upah Rp 50 000 lebih banyak dari upah semula. Berapakah banyaknya pekerja proyek tersebut mula-mula?

[Penyelesaian]

Misalkan jumlah pekerja mula-mula = x , dan

Jumalah upah yang diterima mula-mula = y

xy= 2000 000 ……(1)

(x-2)(y+50 000) = 2000 000 …..(2)

Dari (2):

xy+50000x-2y-100000=2000 000

2000 000 +50000x-2y-100000=2000 000

50000x-2y=100000

25000x-y=50 000

y= 25000x-50000 ……………(3)

Subtitusikan (3) ke (1):

xy= 2000 000 ……(1)

x(25000x-50000)= 2000 000

$\\25000x^2-50000x-2000000=0\\x^2-2x-80=0\\(x-10)(x+8)=0\\x=10\, ;\, x=-8\, \, (tidak\, memenuhi))$

Jadi jumlah pekerja mula-mula adalah 10 orang.

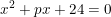3.Persamaan kuadrat $\small x^2+px+q=0$ mempunyai dua buah akar yang sama dan salah satu akar $x^2+px+24=0$ adalah 6, tentukanlah nilai q.

[Penyelesaian]

Salah satu akar dari 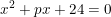$x^2+px+24=0$ adalah 6 maka:

$6^2+6x+24=0$

6p=-60

p=-10

$x^2+px+q=0$ mempunyai dua buah akar yang sama, maka:

syarat , D = 0

$\\b^2-4ac=0\\p^2-4q=0$

100-4q=0

4q=100

q=25

4.Tentukan interval nilai a agar kedua akar $x^2+(a+1)x+(2a-1)=0$ tidak real (khayal)

[Penyelesaian]

Agar kedua akar $x^2+(a+1)x+(2a-1)=0$ tidak real haruslah dipenuhi,

$\\ \Leftrightarrow D<0\\\Leftrightarrow b^2-4ac<0\\\Leftrightarrow (p+1)^2-4\times (2p-1)<0\\ \Leftrightarrow p^2+2p+1-8p+4<0\\\Leftrightarrow p^2-6p+5<0\\\Leftrightarrow (p-5)(p-1)<0\\ \therefore \,{\color{Red} 1<p<5}$

5. Jika akar-akar dari 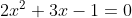$2x^2+3x-1=0$ adalah α (alfa) dan β (beta), tentukanlah nilai dari :

$\\(a)\, \alpha^{2} +\beta^{2}\\(b)\, \alpha ^{3}+\beta ^3$

[Penyelesaian]

$\alpha +\beta =\frac{-b}{a}=\frac{- 3}{2}\, ;\, \, \alpha \beta =\frac{c}{a}=\frac{-1}{2}$

$\small \\(a)\, \alpha ^2+\beta ^2=(\alpha +\beta)^2- 2\alpha\beta\\\\\Leftrightarrow \left ( \frac{-3}{2} \right )^{2}-2\times \left ( \frac{-1}{2} \right )\\\\\Leftrightarrow \frac{9}{4}+1={\color{Red} \frac{13}{4}}$

$\\(b)\, \alpha ^3+\beta ^3=(\alpha +\beta)^3-3\alpha\beta (\alpha +\beta )\\\\\Leftrightarrow \left ( \frac{-3}{2} \right )^{3}-3\times\left ( \frac{-1}{2} \right )\times\left ( \frac{-3}{2} \right )\\\\\Leftrightarrow \left ( \frac{-27}{8} \right )+\left ( \frac{9}{4} \right )={\color{Red} \left ( \frac{-45}{8} \right )}$

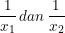6. Jika akar-akar dari $\small x^2+4x-7=0\, \, adalah\, \, x_{1}\, dan\, x_{2}$ , tentukanlah persamaan kuadrat baru yang mempunyai akar-akar $\frac{1}{x_{1}}\, dan\, \frac{1}{x_{2}}$ (berkebalikan).

[Penyelesaian]

$\\x_{1}+x_{2}=\frac{-b}{a}=-4\, \, dan\, \, x_{1}x_{2}=-7\\\\\Leftrightarrow \frac{1}{x_{1}}+\frac{1}{x_{2}}=\frac{x_{1}+x_{2}}{x^{1}x_{2}}=\frac{4}{7}\\\\\Leftrightarrow \frac{1}{x_{1}x_{2}}=\frac{-1}{7}$
$\\ Persamaan\, kuadrat\, baru:\\\Leftrightarrow x^2-\left ( \frac{1}{x_{1}}+\frac{1}{x_{2}} \right )x+\frac{1}{x_{1}x_{2}}=0\\\\\Leftrightarrow x^2-\frac{4}{7}x-\frac{1}{7}=0\\\\\Leftrightarrow {\color{Red} 7x^2-4x-1=0}$

Ada yang ingin ditanyakan berkenaan dengan soal-soal atau materi dalam artkel ini, tinggalkan komentar anda dibagian kolom komentar. Saya ucapkan terimakasih telah berkunjung ke blog saya yang sederhana ini jangan lupa like fanspage facebooknya ya, agar kita bisa berdiskusi tentang soal-soal persamaan kuadrat.