Aturan Sinus Dan Cosinus – Media Masyarakat

Daftar Isi

Aturan Sinus dan Cosinus pada Trigonometri

Aturan sinus dan cosinus sungguh diharapkan dalam menjumlah segi segitiga atau sudut dalam segitiga yang belum dimengerti. Setelah mempelajari rumus-rumus dan contoh soal nanti akan dimengerti pentingnya aturan sinus dan cosinus.

Aturan Sinus Dalam Segitiga

Dalam setiap segitiga sembarang ABC , dengan sisi AB = c, segi AC = b dan AC = a maka akan selalu berlaku:

Rumus diatas memakai segitiga dibawah ini:

Pembuktian Aturan Sinus dan Cosinus

Pembuktian Aturan Sinus

Untuk membuktikan rumus aturan sinus diatas, Buat segitiga lancip ABC lihat gambar 1. Garis CR, BQ, dan AP yaitu garis tinggi pada segi c, segi b dan segi a.

Gambar 1

Lihat Δ ACR :
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Lihat Δ BCR:
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Dari persamaan (1) dan (2), didapat:
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Lihat Δ BAP:
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Lihat Δ CAP:
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Dari persamaan (4) = (5), didapat:

$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Dari persamaan (3) = (6), didapat:
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Persamaan yang diperoleh terakhir inilah yang disebut aturan sinus.

Contoh Soal dan Pembahasan Aturan Sinus

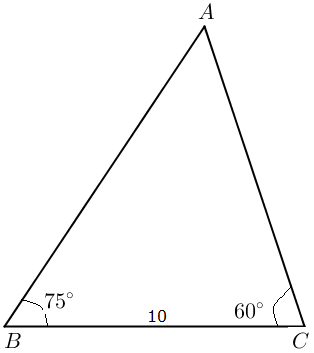
1). Dengan menggunakan aturan sinus hitunglah c pada ΔABC Jika a = 10,∠ B = 75° , dan ∠ C = 60°

[Penyelesaian]

Hitung, ∠ A = 180⁰ – 75⁰ – 60⁰ = 45⁰

Dengan menggunakan hukum sinus, maka:
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

2). Tentukanlah ∠ C pada ΔABC bila b = √ 2 , c = 2 dan ∠ B = 30°

[Penyelesaian]

Dengan memakai aturan sinus, maka:
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Penggunaan hukum sinus

Kita harus memahami penggunaan hukum sinus dan cosinus, kapan kedua rumus tersebut digunakan dalam menyelesaikan soal. Kemungkinan unsur-komponen yang diketahui yaitu:

Sisi, sudut, sudut
Sudut, segi, sudut
Sisi, segi, sudut

Dengan memahami unsur-bagian yang mungkin diketahui akan gampang untuk menganalisa aturan mana yang dipakai dari aturan sinus dan kosinus.

Aturan Cosinus

Pada setiap segitiga ABC senantiasa berlaku aturan cosinus yakni:

Jika pada segitiga ABC jika ketiga sisinya sudah dikenali, maka besar masing-masing ketiga sudutnya mampu dijumlah menggunakan rumus-rumus dibawah ini:

Pembuktian hukum cosinus

Perhatikan ΔABC dibawah ini, garis tinggi CD = h pada sisi c.

Lihat ΔBCD , dengan teorema phytagoras diperoleh:
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Lihat ΔACD:
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Sehingga,
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Subtitusikan AD = b cosA , dan BD = c – b cosA ke persamaan (1), sehingga diperoleh:

$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Persamaan yang terakhir inilah yang disebut aturan cosinus atau dalil cosinus.

Contoh soal Dan pembahasan hukum Cosinus

1). Tentukan nilai a pada ΔABC jika diketahui b = 2, c = 3 dan ∠A = 60°

[Penyelesaian]

Dengan menggunakan hukum cosinus,
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$ ,

2). Pada ΔABC diketahui panjang sisi a = 3 cm , panjang segi b = 5 cm dan c = 7 cm. Tentukan besar ∠C

[Penyelesaian]

Dengan memakai hukum cosinus sudut maka,
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Dengan melaksanakan dan berlatih teladan-teladan diatas tentu kita akan makin hebat kapan hukum sinus dan cosinus dipakai.

Aturan sinus dan cosinus – Luas Segitiga

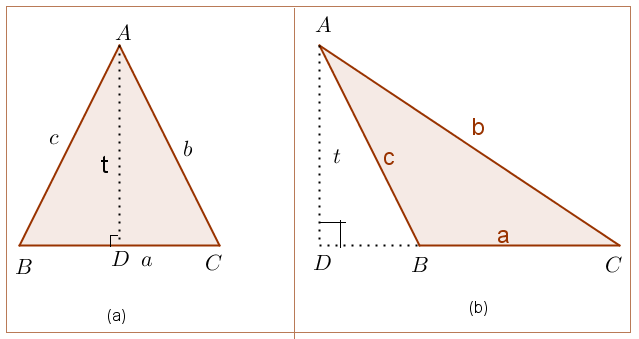
Luas ΔABC baik itu segitiga lancip maupun segitiga tumpul mampu ditentukan dengan rumus luas segitiga .Perhatikan gambar segitiga lancip dan segitiga tumpul dibawah ini:

Maka luas segitiga (a) dan (b) pada gambar diatas dapat diputuskan dengan rumus luas segitiga, ialah:

Contoh Soal Dan Pembahasan Luas Segitiga

1). Dalam ΔABC , Panjang sisi a = 4 cm , panjang segi b = 6 cm dan besar ∠C = 30° Hitunglah luas ΔABC.

[Penyelesaian]

Dengan memakai rumus luas segitiga maka,
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

2). Jajargenjang ABCD , panjang AB = 8 cm, AD = 6 cm dan ∠BAD = 60° .Hitunglah Luas jajargenjang ABCD

[Penyelesaian]

Hitung Luas ΔBAD terlebih dulu dengan rumus luas segitiga,

Karena ΔBAD kongruen dengan ΔCDB maka luas jajar genjang ABCD:

$\dpi100 \fn_cm \small \\L=L\, \Delta ABD+L\, \Delta CDB\\\\L=12\sqrt3+12\sqrt3 \\\\L=\mathbf24\sqrt3 \, cm^2$ :

Luas segitiga Jika ketiga sisinya Diketahui

Jika dikenali panjang ketiga sisi segitiga dengan panjang sisi masing-masing a, b, dan c maka luasnya ialah:

Dengan S = ½ ´ keliling segitiga ABC atau

$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Contoh soal:

Pada segitiga ABC dimengerti panjang sisi a = 7 cm, panjang sisi b = 8 cm dan c = 9 cm. Tentukan luas segitiga tersebut!

[Penyelesaian]

Tentukan dahulu s :
$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Maka Luas segitiga ABC yaitu:

$Aturan Sinus dan Cosinus pada Trigonometri Aturan Sinus dan Cosinus$

Demikian, supaya bermanfaat dan supaya artikel ini mampu menjadi rujukan dalam mencar ilmu atau pun mengajar ihwal bahan hukum sinus dan cosinus.