
Garis singgung persekutuan luar merupakan salah satu konsep penting dalam matematika yang sering kali membingungkan banyak siswa. Namun, dengan pemahaman yang tepat, rumus-rumus ini bisa dipahami dengan mudah. Dalam artikel ini, kita akan membahas rumus garis singgung persekutuan luar serta contoh penerapannya dalam kehidupan sehari-hari.
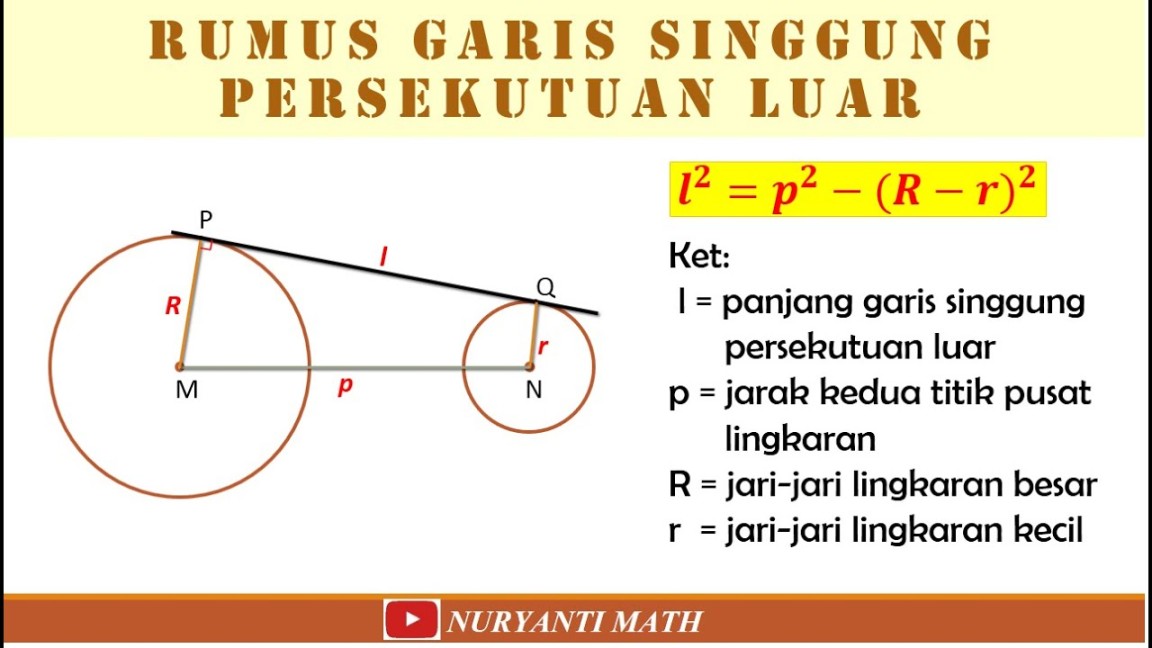
Garis singgung persekutuan luar adalah garis yang menyentuh dua lingkaran secara luar. Garis ini memiliki sifat bahwa garis singgung tersebut tegak lurus dengan radius yang ditarik ke titik singgung. Dengan kata lain, garis singgung persekutuan luar adalah garis yang bersinggungan dengan kedua lingkaran tersebut namun tidak memotong lingkaran tersebut.
Rumus untuk mencari garis singgung persekutuan luar dapat dihitung menggunakan rumus berikut:
1. Rumus Panjang Garis Singgung Persekutuan Luar:
Panjang garis singgung persekutuan luar dapat dihitung menggunakan rumus berikut:
( sqrt{(r1 + r2)^2 + d^2} )
Dimana r1 dan r2 adalah radius dari dua lingkaran yang bersinggungan dan d adalah jarak antara pusat kedua lingkaran.
2. Rumus Sudut yang Dibentuk Oleh Garis Singgung Persekutuan Luar:
Sudut yang terbentuk oleh garis singgung persekutuan luar dan garis yang menghubungkan pusat dua lingkaran dapat dihitung menggunakan rumus berikut:
( theta = frac{1}{2} times arcsinleft(frac{|r1 – r2|}{d}right) )
Sebagai contoh penerapan rumus garis singgung persekutuan luar, kita bisa mengambil contoh dua lingkaran yang bersinggungan dengan radius masing-masing 5 cm dan 3 cm serta memiliki jarak antara pusat kedua lingkaran sebesar 8 cm. Dengan menggunakan rumus-rumus di atas, kita dapat menghitung panjang garis singgung persekutuan luar dan sudut yang terbentuk.
Dari rumus panjang garis singgung, kita dapat menghitung:
( sqrt{(5 + 3)^2 + 8^2} = sqrt{64 + 64} = sqrt{128} approx 11.31 ) cm
Sedangkan untuk menghitung sudut yang terbentuk, kita dapat menggunakan rumus sudut yang telah disebutkan sebelumnya.
Dengan memahami rumus garis singgung persekutuan luar serta contoh penerapannya, kita dapat lebih memahami konsep matematika ini. Penting untuk selalu memahami rumus-rumus ini agar bisa mengaplikasikannya dalam berbagai situasi.
1. Apa itu garis singgung persekutuan luar?
Garis singgung persekutuan luar adalah garis yang menyentuh dua lingkaran secara luar.
2. Bagaimana rumus untuk menghitung panjang garis singgung persekutuan luar?
Panjang garis singgung persekutuan luar dapat dihitung menggunakan rumus ( sqrt{(r1 + r2)^2 + d^2} ).
3. Apa yang dimaksud dengan sudut yang terbentuk oleh garis singgung persekutuan luar?
Sudut yang terbentuk oleh garis singgung persekutuan luar dan garis yang menghubungkan pusat dua lingkaran.
4. Bagaimana contoh penerapan rumus garis singgung persekutuan luar dalam kehidupan sehari-hari?
Contoh penerapan rumus ini bisa ditemui dalam desain pembangunan jembatan atau bangunan lainnya.
5. Mengapa penting untuk memahami rumus garis singgung persekutuan luar?
Memahami rumus ini penting karena dapat membantu dalam menyelesaikan permasalahan matematika yang melibatkan lingkaran.