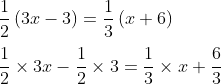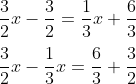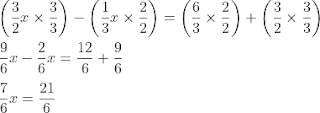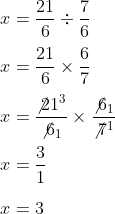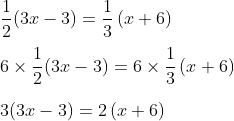Hitunglah Nilai X Dari ½(3X-3)=⅓(X+6)

by

Soal ini adalah versi sistem persamaan linear satu variabel (SPLSV). Mengapa satu variabel? Karena cuma ada satu variabel saja, ialah x.

Jangan resah saat menyaksikan bentuk yang ada serpihan ya!
Santai saja.
Kita akan bahas hingga tuntas, cara apa yang dipakai dan bagaimana menerima nilai x-nya.
Cara yang dipakai
Ada dua cara yang bisa digunakan untuk memecahkan soal ini. Nanti mampu dipilih cara mana yang paling disukai.
Pertama!
Kita akan tetap menggunakan bentuk potongan.
Kedua!
Kita akan menetralisir bentuk kepingan.
Nah…
Sudah tidak sabar menjawab soalnya?
Mari lanjutkan!
Soal
Berikut yaitu soalnya.
Soal :

1. Hitunglah nilai x pada persamaan berikut : ½(3x-3)=⅓(x+6)

Baik, kita mulai dari cara pertama.
Cara pertama

Kita biarkan soalnya dalam bentuk pecahan.

Dan pertama kali, bentuk kurungnya harus dibuka dahulu.
  • Buka kurung masing-masing
  • ½ dikalikan dengan setiap suku di dalam kurung pada ruas kiri
    ½ dikali dengan 3x dan ½ dikalikan dengan -3
  • Untuk ruas kanan, ⅓ dikalikan dengan x dan ⅓ dikalikan dengan 6

  • Sekarang kita kumpulkan yang ada variabel x di ruas kiri.
    Berarti pindahkan ⅓x dipindah ke ruas kiri menjadi -⅓x (dikala pindah ruas maka tanda berganti)
  • Sedangkan -3/2 kita pindah ke ruas kanan sehingga menjadi +3/2
  • Samakan penyebut di masing-masing ruas
  • Ruas kiri penyebutnya 2 dan 3, memiliki arti dijadikan 6.
  • Ruas kanan penyebutnya juga 2 dan 3, berarti dijadikan 6 juga.
Kemudian :
  • Untuk menerima x, kita harus membagi 21/6 dengan 7/6
  • Sederhanakan
    Bagi 21 dan 7 masing-masing dengan 7
  • Bagi 6 dan 6 masing-masing dengan 6

Dan kitapun mendapatkan x = 3.

Itulah cara pertama, dengan tetap menjaga bentuk cuilan. Kita akibatnya menerima nilai x = 3.
Cara kedua

Untuk cara yang ini, kita akan langsung menghilangkan bentuk pecahan demi mempercepat perkiraan.

  Aturan dalam Menggambarkan Diagram Venn
Ketika belahan hilang, soal menjadi tidak terlampau rumit.

Perhatikan soal di atas.

  • Ada dua bentuk potongan, adalah ½ dan ⅓
  • Penyebut masing-masing potongan yaitu 2 dan 3.
  • Kita cari KPK dari kedua penyebut itu, adalah KPK dari 2 dan 3
  • KPK 2 dan 3 adalah 6.
Kemudian :
  • Kalikan 6 di kedua ruas
  • 6×½ = 3
  • 6×⅓ = 2
  • Untuk yang di dalam kurung tidak mengalami pergeseran.

Nah…

Sekarang bentuk kepingan telah hilang.

Selanjutnya, kita buka kurung di ruas kiri dan kanan.
3(3x-3) = 2(x+6)
  • Di ruas kiri
    Kalikan 3 dengan 3x dan kalikan 3 dengan -3
  • Di ruas kanan
    Kalikan 2 dengan x dan kalikan 2 dengan 6
9x-9 = 2x+12
  • Kumpulkan suku yang ada variabel x di sebelah kiri dan yang tidak ada variabel x di sebelah kanan.
  • Pindahkan 2x ke ruas kiri menjadi -2x
  • Pindahkan -9 ke ruas kanan menjadi +9
9x-2x = 12 + 9
7x = 21
  • Untuk menerima x, bagi 21 dengan 7
x = 21 ÷ 7
x = 3.
Nah…
Hasilnya sama.
Kaprikornus silahkan pilih mana yang disukai ya!
Baca juga ya :