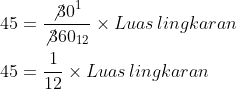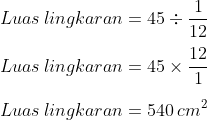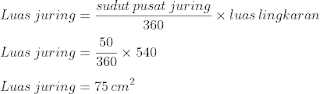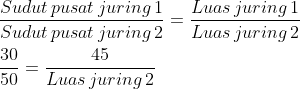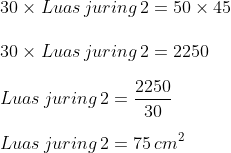Juring Bersudut 30⁰ Memiliki Luas 45 Cm², Maka Luas Juring Yang Sudut Pusatnya 50⁰ Ialah…

by

Ada dua cara yang dapat dipakai untuk mendapatkan balasan soal ini. Kita coba satu per satu dan bandingkan cara mana yang paling favorit ya…

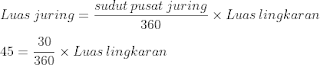
Tetapi, kita harus tahu dahulu rumus mencari luas juring. Rumusnya tidak rumit kok, bisa dihafalkan dengan gampang.
Rumus luas juring
Rumus mencari luas juring yaitu…

Nah…

Itulah rumusnya…
Sekarang kita mampu masuk ke soalnya.
Contoh soal
Mari lihat soalnya.
Soal :

1. Juring dengan sudut sentra 30⁰ luasnya 45 cm², hitunglah luas juring yang sudut pusatnya 50⁰…

Seperti yang telah disebutkan di atas, ada dua cara yang mampu dikerjakan. Kita akan bahas keduanya, perhatikan ya!!

Cara pertama

Untuk cara yang pertama, kita akan mencari luas lingkarannya dulu. Karena pada rumus luas juring ada luas bulat.

Inilah yang dicari dahulu.

Mencari luas bulat

Pada soal dimengerti data :
  • Sudut sentra juring 30⁰ luasnya 45 cm²
  • Inilah data yang akan digunakan untuk menerima luas lingkaran, karena dikenali sudut sentra dan luas juringnya.
  • Masukkan luas juring = 45
  • sudut sentra juring = 30
  • Sederhanakan 30 dan 360, keduanya sama-sama dibagi 30
  • Untuk menerima luas bundar, 45 harus dibagi dengan 1/12
  • Tanda bagi berkembang menjadi kali dan bagian 1/12 dibalik menjadi 12/1
Dan kita menerima luas lingkaran adalah 540 cm²

Mencari luas juring sudut sentra 50⁰

Sekarang kita mampu mencari luas juring yang sudut pusatnya 50⁰ sebab luas lingkaran sudah diketahui.
  • Masukkan sudut sentra juring = 50
  • ganti luas bundar dengan 540 (sesuai hasil perkiraan sebelumnya)
Diperoleh luas juring dengan sudut sentra 50⁰ sebesar 75 cm².
Nah akhir…
Itulah cara yang pertama…
Yaitu memakai rumus luas juring dan kita mesti mencari luas lingkarannya lebih dahulu. Perhatikan langkah-langkahnya ya!!
Cara kedua

Cara yang kedua, kita tidak akan memakai rumus luas juring, melainkan menggunakan perbandingan.

  Penyelesaian persamaan sin (x - 45)° > 1/2√3 untuk 0 ≤ x ≤ 360
Masih ingat dengan topik ini?
Ok mari lihat lagi data pada soal.
  • Sudut sentra juring 1 ialah 30⁰
  • Luas juring 1 yakni 45 cm²
  • Sudut pusat juring 2 adalah 50⁰
Yang ditanyakan : luas juring 2….?
Perbandingan yang dipakai mirip ini.
  • Masukkan data-data di atas ke dalam rumus perbandingan
  • Kalikan silang 30 dengan luas juring 2
  • Kalikan silang juga 50 dengan 45
  • Sehingga kita tidak memiliki bentuk potongan lagi.
Untuk menerima luas juring 2, maka 2250 mesti dibagi dengan 30.
Hasilnya 75 cm².
Nah, kesudahannya sama bukan dengan cara pertama??
Mau pilih yang mana?
Silahkan gunakan yang paling disenangi!!
Baca juga ya :