Sebelum mempelajari program linear lebih lanjut, mari mempelajari dasar-dasar program linear dr akar permasalahan. Program linear mencakupbeberapa desain materi dasar seperti, persamaan linear, tata cara pertidaksamaan linear, & kawasan penyelesaian metode pertidaksamaan linear. Selanjutnya, mari mempelajari perihal pertidaksamaan & tata cara pertidaksamaan linear dua variabel.
A. Pertidaksamaan & Sistem Pertidaksamaan Linear Dua Variabel (SPLDV)
1. Pertidaksamaan Linear Dua Variabel
Jika x & y merupakan variabel,a,b,dan c merupakan bilangan/konstanta, pertidiksamaan linear dapat dituliskan selaku berikut: ax + by < c, ax + by > c, ax + by ≤ c, & ax + by ≥ c.
Contoh bentuk pertidaksamaan linear dua variabel.
1. 2x + 3y < 6
2. 3x + 4y > 12
3. x + y ≤ 10
4. 5x – 2y ≥ 20
Pertidaksamaan-Pertidaksamaan linear dua variabel memiliki penyelesaian yg berupa tempat penyelesaian. Daerah penyelessaian ini merupakan titik-titik (x, y) yg memenuhi pertidaksamaan tersebut.
Perlu diperhatikan:
Dalam materi ini, daerah penyelesaiannya adalah daerah yg DIARSIR.
meskipun di buku/pengajar lain justru sebaliknya. Hal ini tak mengapa, yg terang kita mengerti kawasan penyelesaian dr sistem pertidaksamaan yg ditandai dgn komitmen ditempat siswa berguru.
Daerah penyelesaian ini dapat digambarkan mirip berikut.
Contoh 1
Tentukan daerah solusi dr pertidaksamaan x + y ≤ 10.
Jawaban:
Langkah pertama kita membuat persamaan x + y = 10 (persamaan garis lurus)
Membuat dua titik bantu.
Untuk x = 0, maka y = 10. Diperoleh titik (0, 10)
Untuk y = 0, maka x = 10. Diperoleh titik (10, 0)
Selanjutnya digambar garis sesuai pertidaksamaan x + y ≤ 10.
Gambar yg diarsir adalah kawasan penyelesaian pertidaksamaan x + y ≤ 10. Untuk mengecek/menyelidiki kebenarannya sebgai berikut.
Daerah yg diarsir menampung (0,0). Jika (0,0) kita substitusikan ke x + y ≤ 10 akan diperoleh
0 + 0 ≤ 10. Hal ini sebuah pernyataan yg benar.
Contoh 2
Tentukan daerah penyelesaian dr pertidaksamaan 2x + 3y ≥ 18.
Jawaban:
Langkah pertama kita membuat persamaan 2x + 3y = 18 (persamaan garis lurus)
Membuat dua titik bantu.
Untuk x = 0, maka y = 6. Diperoleh titik (0, 6)
Untuk y = 0, maka x = 9. Diperoleh titik (9, 0)
Selanjutnya digambar garis sesuai pertidaksamaan 2x + 3y ≥ 18.
Daerah yg diarsir ialah tempat penyelesaian pertidaksamaan linear 2x + 3y ≥ 18.
2. Sistem Pertidaksamaan Linear Dua Variabel (SPLDV)
Kita tahu bahwa pada materi yg kemudian dibahas sistem persamaan linear dua variabel. Dalam potensi ini akan dibahas wacana metode pertidaksamaan linear dua variabel. Sistem persamaan linear dua variabel ialah adonan beberapa pertidaksamaan linear dua variabel yg variabel-variabelnya saling berkaitan (variabelnya sama). Dengan demikian dr metode pertidaksamaan tersebut diperoleh penyelesaian dr kedua atau lebih pertidaksamaan itu.
Bentuk biasa tata cara pertidaksamaan linear dua veriabel.
ax + by ≤ c
px + qy ≤ r
Tanda ketidaksamaan dapat meliputi ≤, ≥, <, >.
Perhatikan teladan tata cara pertidaksamaan & penyelesaiannya berikut.
Contoh 1
Diketahui sistem pertidaksamaan berikut.
x + y ≤10
2x + 3y ≤ 24
x ≥ 0,
y ≥ 0
Jawaban:
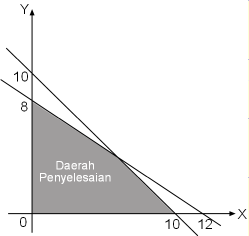
Persamaan x + y = 10 berpotongan terhadap sumbu X & sumbu Y di (10, 0) & (0,10).
Persamaan 2x + 3y = 24 berpotongan kepada sumbu X & sumbu Y di (12, 0) & (0,8).
Titik (0, 0) memenuhi sistem petidaksamaan di atas. sehingga tempat yg menampung (0, 0) merupakan tempat penyelesaian sistem persamaan tersebut.
Sehingga tempat solusi dr SPLDV tersebut mampu digambarkan mirip di bawah ini.
Contoh 2
Diketahui metode pertidaksamaan berikut.
x + y ≥ 8
5x + 3y ≥ 30
x ≥ 0,
y ≥ 0
Jawaban:
Persamaan x + y = 8 berpotongan kepada sumbu X & sumbu Y di (8, 0) & (0,8).
Persamaan 5x + 3y = 30 berpotongan terhadap sumbu X & sumbu Y di (6, 0) & (0,10).
Titik (0, 0) tak menyanggupi metode petidaksamaan di atas sehingga tempat yg menampung (0, 0) bukan merupakan kawasan solusi tata cara persamaan tersebut.
Sehingga tempat penyelesaian dr SPLDV tersebut dapat digambarkan mirip di bawah ini.
Contoh 3
Diketahui tata cara pertidaksamaan berikut.
x + y ≤ 12
2x + 5y ≥ 40
x ≥ 0,
y ≥ 0
Jawaban:
Persamaan x + y = 12 berpotongan terhadap sumbu X & sumbu Y di (12, 0) & (0,12).
Persamaan 2x + 5y = 40 berpotongan terhadap sumbu X & sumbu Y di (20, 0) & (0, 8).
Titik (0, 0) memenuhi sistem petidaksamaan x + y ≤ 12 sehingga daerah yg menampung (0, 0) merupakan daerah solusi pertidaksamaan x + y ≤ 12.
Titik (0, 0) tak menyanggupi tata cara petidaksamaan 2x + 5y ≥ 40 sehingga tempat yg menampung (0, 0) bukan merupakan kawasan penyelesaian pertidaksamaan 2x + 5y ≥ 40.
Sehingga kawasan penyelesaian dr SPLDV tersebut dapat digambarkan mirip di bawah ini.
Demikian klarifikasi ihwal Pertidaksamaan & Sistem pertidaksamaan linear dua variabel. Berikutnya akan dibahas ihwal progam linear di segmen berikutnya sebagai bahan terkait dr materi ini.