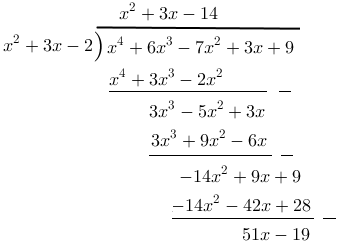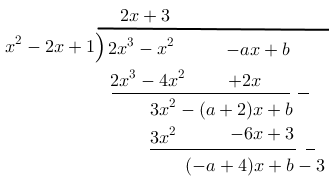Daftar Isi
Pengertian suku banyak matematika
Suku banyakatau polinomial dalam x dan berderajat n yaitu suatu bentuk yang secara umum dituliskan sebagai berikut:
Poin-poin penting dalam suku banyak (polinom):
– □  merupakan bilangan real dan
merupakan bilangan real dan 
– □  merupakan koefisien
merupakan koefisien  merupakan koefisien
merupakan koefisien  ,… , dst. Sedangkan
,… , dst. Sedangkan  disebut konstanta.
disebut konstanta.
– □ Derajat suku banyak ditentukan oleh pangkat tertinggi dari variabel x
– □ Penulisan suku-suku pada suku banyak dimulai dari variabel pangkat tertinggi, diikuti suku-suku dengan pangkat menurun disebut aturan pangkat turun
– □ Suku banyak yang hanya mempunyai satu variabel disebut suku banyak univariabel dan suku banyak dengan lebih dari satu variabel disebut suku banyak multivariabel
Contoh 1:
Tentukan variabel, derajat dan koefisien dari suku banyak 
[Penyelesaian]
Suku banyak diatas berderajat 3, koefisien  adalah 2, koefisien
adalah 2, koefisien  adalah 5, koefisien x adalah -10 dan kontstantanya 7.
adalah 5, koefisien x adalah -10 dan kontstantanya 7.
Menghitung Nilai Suku Banyak
Suku banyak dapat dituliskan dalam bentuk fungsidengan bentuk umum:
Ada beberapa cara menentukan nilai yaitu dengan metode subtitusi dan metode bagan atau skema
Menentukan Nilai Suku Banyak Metode Subtitusi
Menentukan nilai suku banyak dengan metode subtitusi tentu sangat mudah, hanya mengganti veriabel nya dengan nilai tertentu.
Contoh 2:
1. Hitunglah nilai suku banyak , =x^3+3x^2-x+2) untuk setiap nilai xberikut
untuk setiap nilai xberikut
a. x = –2
b. x = a – 1
[Penyelesaian]
Catatan :
Metode subtitusi cocok dipakai untuk menentukan nilai suku banyak dengan bentuk sederhana dan untuk nilai x yang tidak terlalu besar dan x bilangan bulat.
Menentukan Nilai Suku Banyak Metode Bagan atau Skema
Metode bagan atau skema dapat digunakan untuk menentukan nilai semua bentuk suku banyak dan sembarang nilai x ϵ R. Pada dasarnya metode skema merupakan gabungan operasi perkalian dan operasi penjumlahan yang ditampilkan dalam bentuk bagan atau skema
Contoh 3 :
Tentukan nilai setiap fungsi dibawah ini dengan metode skema!
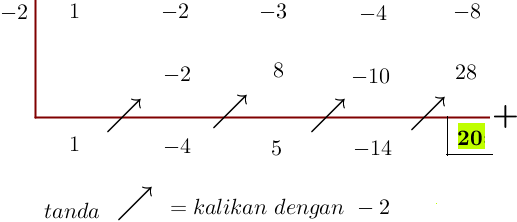
1. Hitunglah f(-2) , untuk =x^4-2x^3-3x^2-4x-8)
[Penyelesaian]
Dengan menggunakan skema atau bagan susun bilangan-bilangan pada baris pertama yang memuat setiap koefisien x mulai dari pangkat tertinggi sampai pangkat terendah
Jadi, nilai f(-2) = 20
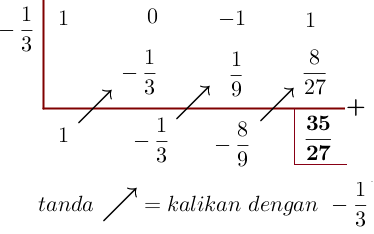
2. Hitunglah ) , untuk
, untuk =x^3-x+1)
[Penyelesaian]
Pada soal ini koefisien x^2 tidak ada, maka tempat koefisiennya dituliskan nol.
Jadi,=\frac{35}{27})
3. Hitunglah =x^2y+x^3y^2+x^2+3y+2) , untuk x = 2
, untuk x = 2
[Penyelesaian]
Suku banyak ini terdiri dari dua variabel yaitu xdan y , suku banyak f(x,y) dipandang sebagai variabel dalam x. Sehingga =y^2x^3+(y+1)x^2+(3y+2))
Bagannya adalah:
Jadi,=8y^2+7y+6})
Kesamaan Suku Banyak
Kesamaan dua suku banyak ditulis f(x) ≡ g(x) , yaitu jika kedua suku banyak mempunyai nilai yang sama untuk setiap variabel x. Sifat kesamaan dua suku banyak dapat dipakai untuk menentukan nilai-nilai suatu bentuk aljabar yang belum diketahui. Simak contoh-contoh dibawah ini:
Contoh 4 :
1. Tentukan nilai a dan b sehingga persamaan berikut berlaku untuk setiap nilai x,
[Penyelesaian]
Bandingkanlah koefisien pada ruas kiri dan ruas kanan,
\\3a^2+b=15\,&space;....(2)&space;\\&space;a^3+c=-7\,&space;....(3)&space;\end{matrix}\right.)
Dari (1), a = –2, subtitusikan a = –2 ke (2) diperoleh b = 3 ,subtitusikan a = –2 ke (3) dieproleh c = 1
Jadi, a = –2 ; b = 3 dan c = 1
Jadi, a = –2 ; b = 3 dan c = 1
2.Tentukan nilai a, b dan c sehingga persamaan berikut merupakan identitas,(x-2)+b(x-2)(x-3)+c(x-3)(x-1)=x)
[Penyelesaian]
Dengan menggunakan metode subtitusi nilai,
&space;\\Jika\,\,&space;\,&space;x=2,\,&space;-c=2\,&space;...(2)&space;\\Jika\,\,&space;\,&space;x=3,\,&space;2a=3\,&space;...(3)) ,
,
Dari (1), (2) dan (3) maka dieproleh:
a = 3/2 ; b = ½ dan c = – 2
a = 3/2 ; b = ½ dan c = – 2
3.Tentukan nilai a, b dan c sehingga persamaan berikut berlaku untuk setiap nilai x,
 ,
,
[Penyelesaian]
(x-2)+bx(x-2)+cx(x-1)}{x(x-1)(x-2)}&space;\\\\\frac{4x-2}{x^3-3x^2+2x}=\frac{a(x^2-3x+2)+b(x^2-2x)+c(x^2-x)}{x(x-1)(x-2)})
x^2+(-3a-2b-c)x+2a}{x^3-3x^2+2x})
Bandingkanlah koefisien pembilang pada ruas kiri dan ruas kanan,
\\&space;-3a-2b-c=4\,&space;....(2)&space;\\&space;2a=-2\,&space;...................(3)&space;\end{matrix}\right.)
Dari (3) a = – 1 subtitusikan a = –1 ke (2) dan (1) lalu eliminasi c diperoleh , b = – 2 dan c = 3
Pembagian Suku Banyak
a. Pembagian Suku Banyak dengan cara Bersusun
Hubungan antara yang dibagi, pembagi , hasil bagi dan sisa pembagian, dapat dituliskan secara umum sebagai berikut:
Yang dibagi = (Pembagi × hasil bagi) + Sisa pembagian
Contoh 5:
Tentukan hasil bagi, dan sisa pembagian soal-soal dibawah ini!
1.  , dibagi oleh
, dibagi oleh 
[Penyelesaian]
Buatlah model pembagian seperti dibawah ini:
Hasil bagi : 2x + 6 dan sisa : 7x + 8
Jadi, (2x+6)+7x+8})
2.  , dibagi x-3
, dibagi x-3
[penyelesaian]
Karena koefisien  tidak ada maka tempat koefisiennya ditambahkan nol, buatlah model pembagian seperti dibawah ini:
tidak ada maka tempat koefisiennya ditambahkan nol, buatlah model pembagian seperti dibawah ini:
Hasil bagi : dan sisa : 0
dan sisa : 0
Jadi, (x^3+3x^2+9x+27)})
3.
[penyelesaian]
Buatlah model pembagian seperti dibawah ini:
Hasil bagi : x – 2y – 1 dan sisa : y – 4
b.Pembagian Suku Banyak dengan Metode Horner
Pembagian suku banyak dengan metode horner ada dua macam pembagi, yaitu:
- Pembagi berbentuk linier (x – k) dan bentuk (ax + b)
- Pembagi berbentuk kuadrat ,
Suku banyak Metode Horner pembagi (x – k)
Misalkan suku banyak yang dibagi f(x) , pembagi (x – k), hasil bagi H(x) dan sisa pembagian S maka persamaan rumusnya adalah:
F(x) = (x – k) × H(x) + S
Contoh 6:
Dengan metode horner tentukan hasil bagi dan sisa pembagian suku banyak berikut!
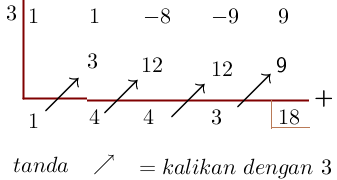
1.  dengan x – 3
dengan x – 3
[Penyelesaian]
Buat terlebih dahulu skemanya,
Berdasarkan bagan diatas, hasil bagi :  dan Sisa : 18
dan Sisa : 18
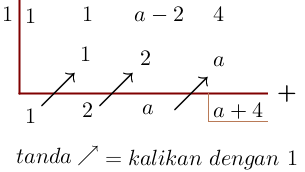
2. Diketahui suku banyak =x^3+x^2+(a-2)x+4) dibagi (x – 1) sisanya – 5 , Tentukanlah nilai a.
dibagi (x – 1) sisanya – 5 , Tentukanlah nilai a.
Buat terlebih dahulu skemanya,
Dari bagan diatas Sisa : a + 4, maka
a + 4 = – 5, jadi a = – 9
Suku banyak Metode Horner pembagi (ax + b)
Misalkan suku banyak yang dibagi f(x) , pembagi (ax +b), hasil bagi H(x) dan sisa pembagian S maka persamaan rumusnya adalah:
Contoh 7:
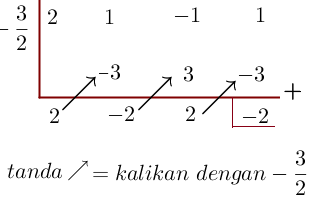
Tentukan hasil bagi dan sisa pembagian =2x^3+x^2-x+1) dengan 2x + 3
dengan 2x + 3
[Penyelesaian]
Dengan metode horner , buat terlebih dahulu skemanya,
Jadi hasil bagi : =\frac{2x^2-2x+2}{2}=\mathbf{x^2-x+1}) dan sisa : – 2
dan sisa : – 2
Suku banyak Metode Horner pembagi berbentuk kuadrat
Jika suku banyak f(x) dibagi dengan  , a ≠ 0 atau berbentuk fungsi kuadrat maka hasil bagi dan sisa tidak bisa ditentukan dengan metode horner , tetapi bisa diselesaikan dengan metode bersusun seperti pada contoh dibawah ini:
, a ≠ 0 atau berbentuk fungsi kuadrat maka hasil bagi dan sisa tidak bisa ditentukan dengan metode horner , tetapi bisa diselesaikan dengan metode bersusun seperti pada contoh dibawah ini:
1.  , dibagi
, dibagi 
[Penyelesaian]
Buatlah model pembagian seperti dibawah ini:
Jadi, Hasil bagi :  dan Sisa : 51x – 19
dan Sisa : 51x – 19
2.Jika  dibagi
dibagi  , sisanya 3x+2 hitunglah nilai a dan b
, sisanya 3x+2 hitunglah nilai a dan b
[Penyelesaian]
Buatlah model pembagiannya:
Karena sisanya 3x + 2, maka
(– a + 4) x + b – 3 = 3x + 2
Bandingkanlah ruas kiri dengan ruas kanan,
– a + 4 = 3 ….. (1)
b – 3 = 2 ……(2)
Dari (1) dan (2),
a = 1 ; b = 5
Dari contoh-contoh diatas pembagian suku banyak dengan metode horner hanya dapat dilakukan jika yang dibagi berbentuk linier, jika yang dibagi berbentuk kuadrat maka pembagian suku banyak dengan metode bersusun.

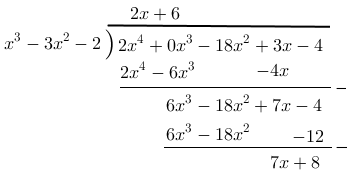
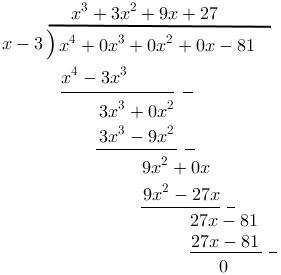
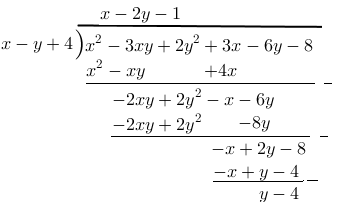
.png)