Daftar Isi
Pengertian Standar Deviasi
Statistika yaitu ilmu yang mempelajari wacana data maupun persebarannya.
Dalam statistika, kita akan mendengar perumpamaan nilai tengah (median), nilai terbanyak (modus), rata-rata (mean), simpangan baku, quartil, persentil, variansi, kriteria deviasi, dan lainnya.
Pada peluang ini akan dibahas perihal tolok ukur deviasi. Standar deviasi yaitu salah satu nilai statistik yang digunakan untuk memilih bagaimana persebaran data dalam suatu sampel, dan seberapa akrab unsur data-data yang ada dengan mean dari sampel tersebut.
Dalam pemakaiannya, standar deviasi berfungsi untuk memilih seberapa heterogen unsur data yang terdapat dalam sebuah data. Semakin besar selisihnya dengan mean, kian heterogen data yang terdapat dalam populasi/sampel.
Cara mengkalkulasikan standar deviasi
Menghitung patokan deviasi dapat dibedakan menjadi 2 cara, yakni cara menghitung patokan deviasi data individu dan data golongan. Untuk penghitungan data individu dapat dijalankan dengan cara di bawah ini:
- Mencari mean data individu
- Menghitung selisih tiap data individu dengan mean
- Masukkan data ke rumus
Kemudian untuk penghitungan data golongan dapat dilaksanakan dengan cara berikut ini:
- Mencari mean dari data golongan
- Menghitung selisih nilai tengah data dengan mean
- Masukkan data ke rumus
Untuk menjumlah rata-rata dari data populasi maupun sampel, mampu menggunakan rumus di bawah ini:
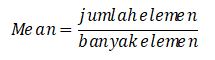
Rumus Standar Deviasi
Dalam pembentukkan rumusnya, patokan deviasi ialah akar kuadrat dari variansi, yang mana variansi itu sendiri dicari dengan menjumlah selisih dari setiap komponen data dengan mean data tersebut.
Variansi dibedakan menjadi dua (variansi populasi (σ2) dan variansi sampel (S2)), sehingga hal tersebut pun berlaku pada patokan deviasi yang merupakan akar dari variansi adalah tolok ukur deviasi populasi (σ) dan persyaratan deviasi sampel (S).
Rumus kriteria deviasi populasi yaitu selaku berikut:
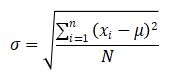
Dengan xi = data ke-i, μ= mean data populasi, dan N = jumlah elemen data populasi. Kemudian rumus kriteria deviasi sampel adalah sebagai berikut:
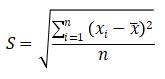
Dengan xi = data ke-i, ͞x σ2 = mean data sampel, dan n = jumlah elemen data sampel.
Contoh Soal Standar Deviasi
Diketahui data nilai matematika 10 siswa kelas 2 Sekolah Menengan Atas 1 Purbalingga yakni: 89; 54; 98; 76; 87; 87; 82; 90; 78; 80. Hitunglah persyaratan deviasinya!
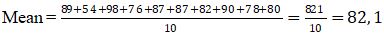
Data di atas ialah data sampel, maka:
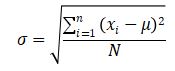
| x | ͞x | ͞x2 |
| 89 | 6.9 | 47.61 |
| 54 | -28.1 | 789.61 |
| 98 | 15.9 | 252.81 |
| 76 | -6.1 | 37.21 |
| 87 | 4.9 | 24.01 |
| 87 | 4.9 | 24.01 |
| 82 | -0.1 | 0.01 |
| 90 | 7.9 | 62.41 |
| 78 | -4.1 | 16.81 |
| 80 | -2.1 | 4.41 |
| jumlah | 1258.9 |
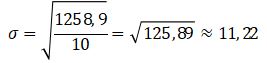
Kaprikornus, kriteria deviasi dari data nilai matematika 10 siswa kelas 2 Sekolah Menengan Atas 1 Purbalingga yaitu 11,22.
Standar Deviasi Excel
Penghitungan kriteria deviasi dari sebuah data mampu dilakukan dengan cara manual memakai rumus yang telah disebutkan di atas.
Selain itu, kita dapat memanfaatkan aplikasi Microsoft office excel yang ialah aplikasi yang dipakai untuk manipulasi data.
Penggunaan aplikasi excel pun dapat dibedakan menjadi dua cara, yaitu cara semi manual dan cara otomatis.
Cara semi manual ialah mengkalkulasikan dengan excel tetapi masih terpaku pada rumus bakunya, sedangkan cara otomatis yakni dengan menggunakan rumus pada excel itu sendiri.
Cara otomatis dapat dilaksanakan dengan langkah-langkah seperti berikut ini:
- Input data pada excel secara lengkap
- Blok data yang sudah diinput
- Gunakan fungsi STDEV.S(Number 1: Number n), number n = elemen terakhir dalam data tersebut
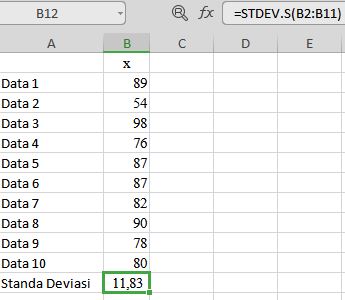
Setelah mengetahui cara menghitung standar deviasi menggunakan excel, dibutuhkan siswa tetap memakai cara manual biar makin dapat memahami materi dan cara penghitungannya.