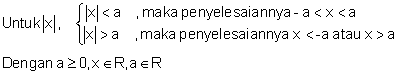Soal Pertidaksamaan Nilai Mutlak – Blog Ilmu Pengetahuan

Soal Pertidaksamaan Nilai Mutlak – Ini memang kami sampikan untuk anda semua alasannya di situs kunci balasan akan memberikan pembahasan lengkap bukan cuma bahan Soal Pertidaksamaan Nilai Mutlak ini saja tetapi aneka macam dari soal Umum, Soal Sekolah Dasar, Soal MI, Soal SMP, Soal MTs, Soal Sekolah Menengan Atas MA, Soal Sekolah Menengah kejuruan, Hingga Perguruan Tinggi. Tentunya dengan hal ini situs ini akan menawarkan kelengkapan buat anda bisa belajari pribadi untuk materi teladan Soal tersebut.

Untuk Postingan kali ini kami bagikan secara pribadi ihwal pembahasan Soal Pertidaksamaan Nilai Mutlak sehingga dengan Soal Pertidaksamaan Nilai Mutlak ini maka anda bisa eksklusif pelajari soal soal tersebut. Oya untuk situs kunci balasan juga memperlihatkan Bank Soal yang ada di positingan ini dimana semua artikel dan bahan soal yang kami update saban hari mampu dilihat di postingan Bank Soal yang suda ada di sidebar dan header dari situ ini.

Anda bisa menyaksikan semua soal-soal tersebut lengkap tinggal pilih bahan soal yang anda ingin pelajari. Karena untuk Bank Soal tersebut ialah mencakum semua isi konten di situs kunci tanggapan.

Tidak usa usang-usang maka peroleh Soal Pertidaksamaan Nilai Mutlak yang kami posting dibawah ini agar bisa bermainfaat buat anda semua yang saat ini ingin memelajari Soal Pertidaksamaan Nilai Mutlak ini.

Soal Pertidaksamaan Nilai Mutlak

Menyelesaikan pertidaksamaan nilai mutlak caranya nyaris sama dengan persamaan nilai mutlak. hanya saja berlawanan sedikit pada tanda ketidaksamaannya. Langkah-langkah selanjutnya mirip menyelesaikan pertidaksamaan linear atau kuadrat satu variabel .
Pertidaksamaan mutlak dapat digambarkan selaku berikut.

Apabila fungsi di dalam nilai mutlak berupa ax + b maka pertidaksamaan nilai mutlak dapat dituntaskan mirip berikut.

Lebih jelasnya perhatikan contoh berikut ini.

Contoh
Tentukan himpunan penyelesaian dari Pertidaksamaan nilai mutlak berikut ini.

Jawaban
1. Cara menyelesaikan pertidaksamaan mutlak ini sebagai berikut.
    -9 < x+7 < 9
    -9 – 7 < x < 9 - 7
       -16 < x < 2
   Kaprikornus, himpunan penyelesaiannya yaitu x/ -16 < x < 2

2. Cara menyelesaikan pertidaksamaan mutlak ini dibagi menjadi dua bab.
   (*) 2x – 1 >= 7
             2x >= 7 + 1
             2x >= 8
               x >= 4

(**) 2x – 1 <= -7
             2x   <= -7 + 1
             2x   <= -6
               x   <= -3

    Makara, himpunan penyelesaiannya adalah x/ x <= -3 atau x >= 4

3. Kalau dalam bentuk soal ini, langkah menuntaskan pertidaksamaannya dengan mengkuadratkan kedua ruas.
amati proses berikut ini.

(x + 3)² <= (2x – 3)²

(x + 3)² – (2x – 3)² <= 0

(x + 3 + 2x – 3) – (x + 3 – 2x + 3) <= 0 (ingat: a² – b² = (a+b)(a-b))

x (6 – x) <=0

Pembuat nol yakni x = 0 dan x = 6

Soal Matematika Akpol

Mari selidiki memakai garis bilangan

Oleh alasannya batasnya <= 0, maka penyelesaiannya ialah x <=0 atau x >=6.

Kaprikornus, himpunan penyelesaiannya yakni x/ x <= 0 atau x >= 6.

Mari selidiki memakai garis bilangan

Oleh alasannya adalah batasnya <= 0, maka penyelesaiannya yaitu x <=0 atau x >=6.

Makara, himpunan penyelesaiannya yakni x/ x <= 0 atau x >= 6.

4. Menyelesaikan pertidaksamaan nilai mutlak seperti ini lebih gampang memakai cara menjabarkan definisi.
Prinsipnya ialah batas-batas-batasan pada fungsi nilai mutlaknya.
Perhatikan pada 3x + 1 dan 2x + 4.

Dari batasan batasan itu maka mampu diperoleh batasan-batas-batas nilai solusi seperti pada garis bilangan di bawah ini.

Dengan garis bilangan tersebut maka pengerjaanya dibagi menjadi 3 bagian daerah penyelesaian.
1. Untuk batasan x >= -1/3 ……(1)
   (3x + 1) – (2x + 4) < 10
          3x + 1 – 2x- 4 < 10
                 x- 3 < 10
                     x < 13 ..…..(2)

Dari (1) dan (2) diperoleh irisan penyelesaian -1/3 <= x < 13

2. Untuk batas-batas -2<= x < -1/3 ……(1)
    -(3x + 1) – (2x + 4) < 10
          -3x – 1 – 2x – 4 < 10
                 -5x – 5 < 10
   -5x < 15
                               -x < 3
                     x > 3 ..…..(2)

Dari (1) dan (2) tidak diperoleh irisan penyelesaian atau tidak ada solusi.

3. Untuk batas-batas x < -2 ……(1)
   -(3x + 1) + (2x + 4) < 10
         -3x – 1 + 2x + 4 < 10
              -x + 3 < 10
   -x < 7
                        x > -7 ..…..(2)

Dari (1) dan (2) diperoleh irisan solusi -7 < x < -2.

Makara, himpunan penyelesaiannya ialah x/ -1/3 <= x < 13 atau -7 < x < -2.

√ Soal Sosiologi Kelas 10 Cuilan Sosiologi Sebagai Ilmu

Perhatikan acuan Pertidaksamaan mutlak yang lain berikut.

sumber: imathsolution.blogspot.co.id