Soal Normalitas

Soal Normalitas – Tentunya dengan Soal Normalitas yang kami sampikan ini akan mampu menciptakan anda mampu mengetahui dan memahami Soal Normalitas yang kami sampikan untuk anda semua. Soal yang kami berikan juga akan memberikan pembahasaan dan juga kunci jawabannya sehingga anda tidak perlu kawatir wacana Soal Normalitas yang kami sampaikan tersebut.

Ini akan sangat membuat lebih mudah untuk anda semua yang ingin belajar Soal Normalitas tersebut. Disini admin kunci balasan memberikan berbagai soal-soal dan pembahasan untuk bisa anda pelajari juga sehingga anda mengetahui wacana soal yang ketika ini anda ingin pelajari.

Untuk selengkapnya wacana Soal Normalitas tersebut kau bisa simak dibawah ini selengkapnya buat anda semua, supaya bisa menjadi manfaat untuk pelajaraan anda ketika ini.

Uji normalitas data ialah bentuk pengujian wacana kenormalan distribusi data. Tujuan dari uji ini ialah untuk mengenali apakah data yang terambil ialah data terdistribusi wajar atau bukan.
Maksud dari terdistribusi wajar yaitu data akan mengikuti bentuk distribusi normal di mana data memusat pada nilai rata-rata dan median.
Rumus yang digunakan untuk uji normalitas ialah rumus kai kuadrat (chi kuadrat).

1. Merumuskan hipotesis
Ho    : data berdistribusi normal
Ha    : data tidak berdistribusi wajar
2. Menentukan nilai uji statistik

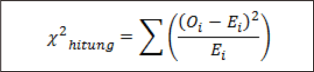
3. Menentukan taraf aktual (α)
Untuk mendapatkan nilai chi kuadrat tabel:

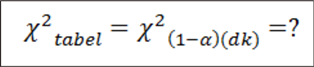
4. Menentukan standar pengujian hipotesis

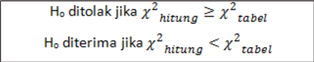
5. Memberikan kesimpulan

Diketahui data skor 32 siswa dalam menyelesaikan soal-soal matematika pada try out di sebuah panduan mencar ilmu.

Ujilah normalitas dari data tersebut!

Penyelesaian:
Langkah 1: Merumuskan hipotesis
Ho : data berdistribusi wajar
Ha : data tidak berdistribusi wajar
Langkah 2: Menentukan nilai uji statistik
Jangkauan (J) = data terbesar – data terkecil
–>  95 – 32
–>  63
Banyak kelas (k) = 1 + 3,3 log n
–>  1 + 3,3 log 32
–>  1 + 4,97
–>  5,97 (diambil k = 6)
panjang kelas = J : k
–>  63 : 6
–>  10,5 (diambil p = 11)
Selanjutnya, data di atas digunakan untuk membuat “tabel A” di bawah ini.

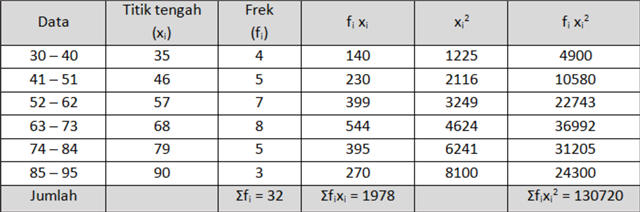
Selanjutnya, mencari rata-rata dan tolok ukur deviasi.

Selanjutnya, menciptakan dan melengkapi “tabel B” berikut. Perhitungannya diterangkan di bawah.

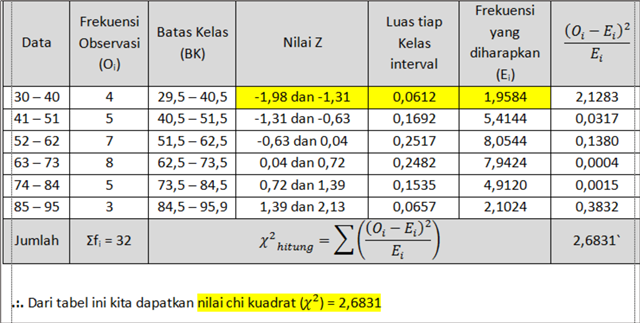
Bagaimana cara mendapatkan “nilai Z” pada tabel B di atas?

Kita ambil Batas Kelas (BK) pada baris pertama ialah: 29,5 – 40,5

Lakukan seperti itu seterusnya, untuk batasan kelas yang lain. Dan peroleh semua nilai Z.
Bagaimana cara mendapatkan “Luas tiap kelas interval” pada tabel B di atas ?
Baiklah, prosedur perkiraan diterangkan di bawah tabel ini.

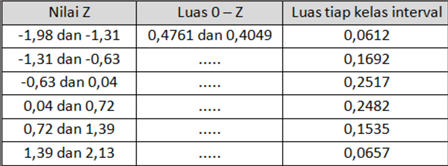
Kaprikornus begini, sesudah mendapatkan “nilai Z”, carilah “Luas 0 – Z” menggunakan tabel Z.
Untuk nilai Z = -1,98, dilihat di tabel Z didapat 0,4761.

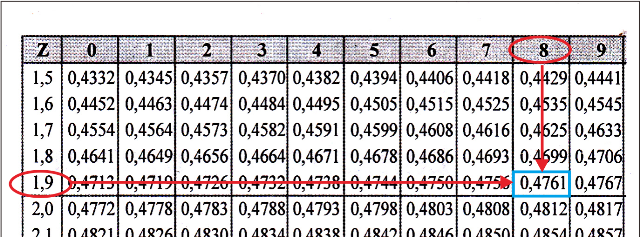
Untuk nilai Z = -1,31, dilihat di tabel Z didapat 0,4049.

Sekali lagi, bagaimana mencari “Luas tiap kelas interval” ?
Kita ambil “Luas 0 – Z” pada baris pertama yakni: 0,4761 dan 0,4049.
Maka, Luas tiap kelas interval  0,4761 – 0,4049 = 0,0612

Lanjutkan menjumlah “Luas tiap kelas interval” pada baris yang selanjutnya.
Bagaimana mencari frekuensi yang diharapkan (E_i) pada tabel B di atas?

Kita ambil “Luas tiap kelas interval” pada baris pertama.
E_i   = Luas tiap kelas interval × n (jumlah responden)
= 0,0612 × 32
= 1,9584
Lakukan begitu untuk baris ke-2, ke-3, dan seterusnya.
.:. Pada tahap ini, kita sudah final menciptakan dan melengkapi tabel B tadi.

Langkah 3: Menentukan taraf kasatmata (α)

Ikuti langkah-langkah berikut:

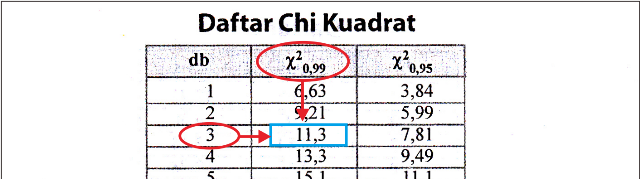
Langkah 4: Menentukan tolok ukur  pengujian hipotesis

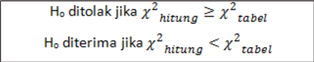
Berdasarkan perkiraan pada tabel diperoleh nilai :

Maka Ho diterima.
Langkah 5: Memberikan kesimpulan
Karena Ho diterima. Artinya, data skor siswa dalam menyelesaikan soal-soal try out matematika di sebuah bimbingan berguru berdistribusi wajar .

SUMBER: slashedmoon.wordpress.com