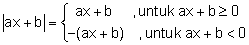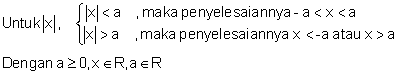Soal Nilai Mutlak

Soal nilai mutlak – Tentunya dengan Soal nilai mutlak yang kami sampikan ini akan bisa membuat anda mampu memahami dan mengetahui Soal nilai mutlak yang kami sampikan untuk anda semua. Soal yang kami berikan juga akan memperlihatkan pembahasaan dan juga kunci jawabannya sehingga anda tidak perlu kawatir wacana Soal nilai mutlak yang kami sampaikan tersebut.

Ini akan sungguh mempermudah untuk anda semua yang ingin berguru Soal nilai mutlak tersebut. Disini admin kunci balasan memperlihatkan berbagai soal-soal dan pembahasan untuk bisa anda pelajari juga sehingga anda mengetahui ihwal soal yang dikala ini anda ingin pelajari.

Untuk selengkapnya tentang Soal nilai mutlak tersebut kamu mampu simak dibawah ini selengkapnya buat anda semua, semoga bisa menjadi faedah untuk pelajaraan anda ketika ini.

Menyelesaikan Persamaan Mutlak

Nilai mutlak sebuah bilangan mampu diartikan jarak antara bilangan tersebut dari titik nol(0). Dengan demikian jarak senantiasa bernilai konkret.
Misalnya:
Parhatikan garis bilangan berikut.

Jarak angka 6 dari titik 0 yakni 6
Jarak angka -6 dari titik 0 yaitu 6 
jarak angka -3 dari titik 0 ialah 3
Jarak angka 3 dari titik0 yakni 3.

Dari penjelesan di atas memang terlihat bahwa nilai mutlak suatu bilangan selalu bernilai aktual. 
Berkaitan dengan menentukan nilai mutlak sebuah bilangan, maka muncullah tanda mutlak. Tanda mutlak disimbolkan dengan  garis 2 ditepi sebuah bilangan atau bentuk aljabar.
Misalnya seperti berikut.

Secara umum, bentuk persamaan nilai mutlak mampu dimaknai mirip berikut.

Jika kita mempunyai persamaan dalam bentuk aljabar, maka dapat dimaknai selaku berikut.

Makara, bentuk dasar di atas dpat digunakan untuk membantu menuntaskan persamaan mutlak.
Lebih jelasnya amati contoh-contoh berikut.

Contoh
Tentukan himpunan solusi dari persamaan nilai Mutlak di bawah ini.

Jawaban:
Bentuk-Bentuk persamaan nilai mutlak di atas mampu dituntaskan selaku berikut. Pada prinsipnya, langkah langkah solusi nilai mutlak diusahakan bentuk mutlak berada di ruas kiri. 
1. Pada bentuk ini ada dua penyelesaian.
   (*) x + 5 = 3  , maka  x = 3 – 5 = -2
   (**) x + 5 = -3, maka x = -3 – 5 = -8
  Makara, himpunan penyelesaiannya adalah -2, -8

2.  Pada bentuk ini ada dua solusi.
   (*) 2x + 3 = 5  , maka  2x = 5 – 3
                                       2x = 2  <==>  x = 1
   (**) 2x + 3 = -5  , maka  2x = -5 -3
                                         2x = -8  <==> x = -4
  Jadi, himpunan penyelesaiannya yakni -4, 1

3. Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu x+1. Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bab.
Bagian pertama untuk batasan x+1>= 0 atau x >= -1

Bagian kedua untuk batas-batas x+1< 0 atau x < -1
Mari kita tuntaskan.
(*) untuk x >=-1
     Persamaan mutlak mampu ditulis:
    (x + 1) + 2x = 7
                   3x = 7 – 1
                   3x = 6
                     x = 2 (terpenuhi, karena batasan >= -1)

(**) untuk x < -1
     Persamaan mutlak mampu ditulis:
    -(x + 1) + 2x = 7
        -x – 1 + 2x = 7
                      x = 7 + 1                
                      x = 8 (tidak tercukupi, sebab batasan < -1)

Makara, Himpunan penyelesaiannya yakni 2.

 4. 
Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu 3x + 4. Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan 3x+4>= 0 atau x >= -4/3

Bagian kedua untuk batas-batas 3x+4< 0 atau x < -4/3
Mari kita selesaikan.
(*) untuk x >=-4/3
     Persamaan mutlak mampu ditulis:
    (3x + 4) = x – 8
        3x – x = -8 – 4
             2x =-12
               x = -6 (tidak terpenuhi, karena batasan >= -4/3)
(**) untuk x < -4/3
     Persamaan mutlak mampu ditulis:
    -(3x + 4) = x – 8
        -3x – 4 = x -8
         -3x – x = -8 + 4
              -4x = -4
                 x = 1 (tidak tercukupi, alasannya adalah batas-batas < -4/3)

Kaprikornus, Tidak ada Himpunan penyelesaiannya.

Menyelesaikan Pertidaksamaan Nilai Mutlak
Menyelesaikan pertidaksamaan nilai mutlak caranya hampir sama dengan persamaan nilai mutlak. hanya saja berlainan sedikit pada tanda ketidaksamaannya. Langkah-langkah berikutnya mirip menuntaskan pertidaksamaan linear atau kuadrat satu variabel .
Pertidaksamaan  mutlak dapat digambarkan selaku berikut.

Apabila fungsi di dalam nilai mutlak berbentuk ax + b maka pertidaksamaan nilai mutlak dapat dituntaskan seperti berikut.








Lebih jelasnya perhatikan contoh berikut ini.

Contoh
Tentukan himpunan solusi dari Pertidaksamaan nilai mutlak berikut ini.

Jawaban
1. Cara menyelesaikan pertidaksamaan mutlak ini sebagai berikut.
    -9 < x+7 < 9
    -9 – 7 < x < 9 - 7
       -16 < x < 2
   Kaprikornus, himpunan penyelesaiannya ialah x/ -16 < x < 2

2. Cara menuntaskan pertidaksamaan mutlak ini dibagi menjadi dua bab.
   (*) 2x – 1 >=  7
             2x  >=  7 + 1
             2x  >= 8
               x  >= 4

  (**) 2x – 1 <= -7
             2x   <= -7 + 1
             2x   <= -6
               x   <= -3
  
    Kaprikornus, himpunan penyelesaiannya yaitu x/ x <= -3 atau x >= 4

 3. Kalau dalam bentuk soal ini, langkah menuntaskan pertidaksamaannya dengan mengkuadratkan kedua ruas.
amati proses berikut ini.

4. Menyelesaikan pertidaksamaan nilai mutlak seperti ini lebih gampang memakai cara menjabarkan definisi.
Prinsipnya yaitu batas-batas-batas-batas pada fungsi nilai mutlaknya.
Perhatikan pada 3x + 1 dan 2x + 4.

Dari batasan batasan itu maka dapat diperoleh batasan-batas-batas nilai penyelesaian seperti pada garis bilangan di bawah ini.

Dengan garis bilangan tersebut maka pengerjaanya dibagi menjadi 3 bagian tempat penyelesaian.
1. Untuk batasan x >= -1/3  ……(1)
   (3x + 1) – (2x + 4) < 10
          3x + 1 – 2x- 4 < 10
                         x- 3 < 10
                             x < 13 ..…..(2)

  Dari (1) dan (2) diperoleh irisan solusi -1/3 <= x < 13

  Dari (1) dan (2) tidak diperoleh irisan penyelesaian atau tidak ada penyelesaian.

  Dari (1) dan (2) diperoleh irisan penyelesaian -7 < x < -2.

Makara, himpunan penyelesaiannya yakni x/ -1/3 <= x < 13 atau -7 < x < -2.

Perhatikan pola Pertidaksamaan mutlak yang lain berikut.