Soal Matematika Aritmatika dan Geometri – Kami berikan buat anda untuk mampu mendapatkan secara pribadi soal deret Aritmatikan dan Geometri sehingga anda bisa pelajari secara pribadi alasannya kami berikan dengan pembahasan Soal Matematika Aritmatika dan Geometri secara pribadi, sehingga mempermudah untuk mempelajari dirumah.
Buat Ibu guru dan Bapak guru untuk bisa membangun anak latih maka secara eksklusif peroleh Soal Matematika Aritmatika dan Geometri tersebut disini nantinya tinggal anda serahkan soal yang ada disini dan untuk pembahasan nanti mampu dibahas secara barang dengan para murid nantinya, sehingga semua mampu mengerti ihwal Soal Matematika Aritmatika dan Geometri tersebut.
Soal Matematika Aritmatika dan Geometri ini akan keluar dari Ulangan Harian, UTS, UAS, US dan UN nantinya yang sungguh perlu untuk dipelajari secara pribadi Soal Matematika Aritmatika dan Geometri tersebut dengan sangat gampang sekali.
1. Perhatikan gambar pola berikut!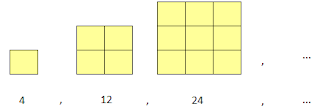
Jika contoh persegi tersebut dibuat dari batang korek api, banyaknya batang korek api pada contoh ke-7 adalah…
a. 40
b. 60
c. 84
d. 112
Pembahasan:
Perhatikan lompatan barisan di atas:
Jadi, banyaknya batang korek api pada acuan ke-7 ada 112
Jawaban: D
2. Segitiga tersebut tersusun atas batang-batang lidi. Banyak segitiga kecil pada teladan ke-7 ialah…
a. 45
b. 49
c. 54
d. 59
Pembahasan:
Perhatikan lompatan barisan bilangan di atas:
Kaprikornus, banyak lidi pada pola ke-7 ada 84
Jawaban: A
3. Dua suku selanjutnya dari teladan: 4, 8 , 14, 22, adalah…
a. 30, 42
b. 30, 44
c. 32, 42
d. 32, 44
Pembahasan:
Kaprikornus, dua suku berikutnya ialah 32 dan 44
Jawaban: D
4. Suku ke-15 dari barisan: 2, 5, 8, 11, 14, … yakni…
a. 41
b. 44
c. 45
d. 47
Pembahasan:
Barisan di atas yaitu barisan aritmatika sebab mempunyai beda yang konstan.
Suku pertama = a = U1 = 2
Beda = b = U2 – U1 = 5 – 2 = 3
Suku ke-15 = U15
Un = a + (n – 1) b
U15 = 2 + (15 – 1) 3
= 2 + 14 . 3
= 2 + 42
= 44
Jawaban: B
5. Suku ke-45 dari barisan bilangan: 3, 7, 11, 15, 19, … adalah…
a. -179
b. -173
c. 173
d. 179
Pembahasan:
Barisan di atas yakni barisan aritmatika, alasannya mempunyai beda yang serupa.
Suku pertama = a = 3
Beda = b = U2 – U1 = 7 – 3 = 4
Un = a + (n – 1) b
U45 = 3 + (45 – 1) 4
= 3 + 44 . 4
= 3 + 176
= 179
Jawaban: D
6. Suku ke-50 dari barisan bilangan: 20, 17, 14, 11, 8, … yakni…
a. -167
b. -127
c. 127
d. 167
Pembahasan:
Barisan di atas merupakan barisan aritmatika, karena mempunyai beda yang serupa.
Suku pertama = a = 20
Beda = b = U2 – U1 = 17 – 20 = -3
Un = a + (n – 1) b
U50 = 20 + (50 – 1) -3
= 20 + 49 . (-3)
= 20 + (-147)
= -127
Jawaban: B
7. Suku ke-8 dari barisan 64, 32, 16, 8, … yakni…
a. ½
b. 1
c. 2
d. 4
Pembahasan:
Barisan di atas ialah barisan geometri, karena mempunyai rasio yang serupa
Suku pertama = a = 64
Rasio = 

Jawaban: A
8. Jumlah 9 suku dari 1 + 2 + 4 + 8 + 16 + … yakni…
a. 255
b. 256
c. 511
d. 512
Pembahasan:
Deret di atas ialah deret geometri, alasannya adalah memiliki rasio yang serupa
Suku pertama = a = 1
Rasio = 

Jawaban: C
9. Diketahui  Nilai U20 yakni..
Nilai U20 yakni..
a. 32
b. 36
c. 42
d. 46
Pembahasan:
Jawaban: A
10. Rumus suku ke-n dari teladan 1, 10, 25, 46, … yaitu …
Pembahasan:
Mari kita uji masing-masing opsi di atas:
a. Opsi A
U2 = 22 (opsi A salah, harusnya U2 = 10)
b. Opsi B
U2 = 10 (pilihan B benar)
Jawaban: B
11. Rumus suku ke-n barisan bilangan 3, 6, 12, 24, adalah…
Pembahasan:
Barisan di atas adalah barisan geometri, sebab mempunyai rasio yang serupa.
Suku pertama = a = 3
Jawaban: C
12. Diketahui barisan bilangan 2, 4, 8, 16, …
Rumus suku ke-n barisan tersebut yakni…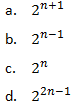
Pembahasan:
Barisan tersebut ialah barisan geometri:
Suku pertama = a = 2
Jawaban: C
13. Rumus suku ke-n dari barisan bilangan 64, 32, 16, 8, … yaitu…
Pembahasan:
Barisan di atas ialah barisan geometri, karena memiliki rasio yang sama
Suku pertama = a = 64
Jawaban: B
14. Rumus suku ke-n dari barisan bilangan 9, 3, 1, 1/3, … ialah…
Pembahasan:
Barisan di atas yaitu barisan geometri, sebab memiliki rasio yang serupa.
Suku pertama = a = 9
Jawaban: C
15. Diketahui barisan aritmatika dengan U5=8 dan U9=20. Suku ke-10 yaitu..
a. -31
b. -23
c. 23
d. 31
Pembahasan:
selanjutnya subtitusikan b = 3 pada persamaan a + 4b = 8
a + 4b = 8
a + 4 (3) = 8
a + 12 = 8
a = 8 – 12
a = -4
jadi, rumus Un = a + (n – 1) b akan menjadi Un = -4 + (n – 1)3
U10 = -4 + (10 – 1) 3
U10 = -4 + 9 . 3
U10 = -4 + 27
U10 = 23
Jawaban: C
16. Suku ketiga dan suku kelima dari barisan aritmatika ialah 17 dan 31. Suku ke-20 dari barisan tersebut ialah..
a. 136
b. 144
c. 156
d. 173
Pembahasan:
Pembahasan:
selanjutnya subtitusikan b = 7 pada persamaan a + 2b = 17
a + 2b = 17
a + 2 (7) = 17
a + 14 = 17
a = 17 – 14
a = 3
jadi, rumus Un = a + (n – 1) b akan menjadi Un = 3 + (n – 1)7
U20 = 3 + (20 – 1) 7
U20 = 3 + 19 . 7
U20 = 3 + 133
U20 = 136
Jawaban: A
17. Suatu barisan geometri memiliki suku ke-2 = 8 dan suku ke-5 = 64. Suku ke-13 dari barisan geometri tersebut yaitu…
Pembahasan:
subtitusikan r = 2 dalam persamaan ar =8
ar =8
a.2 = 8
2a = 8
a = 8:2
a = 4
Jawaban: D
18. Jumlah semua bilangan kelipatan 7 dari 80 sampai 170 adalah…
a. 1.368
b. 1.386
c. 1.638
d. 1.683
Pembahasan:
Bilangan kelipatan 7 ialah barisan aritmatika dengan beda = b = 7
Kita susun dahulu barisannya = 84, 91, 98, 105, … , 168
Suku pertama = a = 84
Beda = b = 7
Kita cari dahulu banyaknya suku dalam barisan tersebut (n)
Un = a + (n – 1 )b (kita gunakan suku terakhir)
168 = 84 + (n – 1) 7
168 = 84 + 7n – 7
168 = 77 + 7n
168 – 77 = 7n
91 = 7n
n = 91 : 7
n = 13
Rumus jumlah:
Jawaban: C
19. Suku ke-3 dan suku ke-7 barisan aritmatika berturut-turut 10 dan 22. Jumlah 30 suku pertama barisan tersebut ialah..
a. 1.365
b. 1.425
c. 2.730
d. 2.850
Pembahasan:
berikutnya subtitusikan b = 3 pada persamaan a + 2b = 10
a + 2b = 17
a + 2 (3) = 10
a + 6 = 10
a = 10 – 6
a = 4
jumlah 30 suku yang pertama (S30)
Jawaban: B
20. Dalam sebuah deret geometri diketahui suku ke-1 = 512 dan suku ke-4 = 64. Jumlah tujuh suku pertama deret tersebut yakni…
a. 1.008
b. 1.016
c. 2.016
d. 2.028
Pembahasan:
Suku pertama = a = 512
jumlah 7 suku pertama (S7) 
Jawaban: B
21. Banyak dingklik pada barisan pertama di suatu gedung pertemuan adalah 10. Banyak bangku pada barisan ke-4 yakni 80 sehingga penyusunan bangku tersebut membentuk deret geometri. Jika dalam gedung itu terdapat 5 baris kursi, banyaknya bangku dalam gedung ialah…
a. 510
b. 420
c. 320
d. 310
Pembahasan:
Penyusunan kursi di atas membentuk barisan geometri.
Suku pertama = a = 10
U4 = 80
n = 5
jumlah kursi dalam 5 baris (S5)
Jawaban: D
22. Suatu basil akan membelah diri menjadi dua setiap menit. Jika banyaknya basil semula ada 6, banyaknya basil setelah 5 menit adalah..
a. 48
b. 96
c. 192
d. 384
Pembahasan:
Banyak bakteri semula = a = 6
Membelah menjadi 2 = rasio = r = 2
Banyak kuman sesudah menit ke-5 (menit ke-0 juga dihitung) mampu diputuskan dengan menjumlah suku ke-(5+1) = suku ke-6
Jawaban: C
23. Dalam setiap 20 menit, amoeba membelah diri menjadi dua. Jika mula-mula ada 50 amoeba, selama 2 jam banyaknya amoeba yaitu…
a. 1.600
b. 2.000
c. 3.200
d. 6.400
Pembahasan:
Banyak amoeba semula = a = 50
Amoeba membelah menjadi 2 = rasio = r = 2
2 jam = 120 menit
n = 1 + (120 : 20)
n = 1 + 6
n = 7
jadi, kita cari U7
Jawaban: C
24. Seorang pegwai kecil menerima honor tahun pertama sebesar Rp3.000.000,00. Setiap tahun honor tersebut naik Rp500.000,00. Jumlah uang yang diterima pegawai tersebut selama sepuluh tahun adalah…
a. Rp7.500.000,00
b. Rp8.000.000,00
c. Rp52.500.000,00
d. Rp55.000.000,00
Pembahasan:
Gaji tahun pertama = a = 3.000.000
Tambahan gaji per tahun = b = 500.000
n = 10 tahun
Sn = n/2(2a + (n – 1)b)
S10 = 10/2(2 x 3.000.000 + (10 – 1) 500.000
= 5 (6.000.000 + 9 x 500.000)
= 5(6.000.000 + 4.500.000)
= 5 x 10.500.000
= 52.500.000
Jawaban: C
25. Amir mempunyai kawat dipotong menjadi 5 bab yang ukurannya membentuk barisan aritmatika. Jika panjang kawat terpendek 15 cm dan terpanjang 23 cm, panjang kawat sebelum dipotong ialah…
a. 85 cm
b. 90 cm
c. 95 cm
d. 100 cm
Pembahasan:
Panjang kawat membentuk barisan aritmatika
Dipotong menjadi 5 = n = 5
Panjang kawat terpendek = a = 15
Panjang kawat terpanjang = U5 = 23
Sn = n/2(a + Un)
S5 = 5/2(15 + 23)
= 5/2(38)
= 5 x 19
= 95
Jawaban: C
26. Sebuah tali diiris menjadi 6 bagian sehingga membentuk deret geometri. Jika panjang pecahan tali terpendek = 3 cm dan pecahan tali terpanjang 96 cm, panjang tali semula adalah…
a. 198 cm
b. 189 cm
c. 179 cm
d. 168 cm
Pembahasan:
Panjang tali membentuk deret geometri
Panjang tali terpendek = a = 3
Potongan tali terpanjang = Un = U6 = 96
Jumlah penggalan = n = 6
Panjang tali semula = Sn = S6
Kita cari terlebih dahulu rasio atau r

Jawaban: B



