Soal Luas Bangun Datar – Tentunya dengan Soal Luas Bangun Datar yang kami sampikan ini akan bisa menciptakan anda mampu mengetahui dan memahami Soal Luas Bangun Datar yang kami sampikan buat anda semua. Soal yang kami berikan juga akan menawarkan pembahasaan dan juga kunci jawabannya sehingga anda tidak butuhkawatir wacana Soal Luas Bangun Datar yang kami sampaikan tersebut.
Ini akan sangat memudahkan buat anda semua yang ingin mencar ilmu Soal Luas Bangun Datar tersebut. Disini admin kunci balasan memberikan aneka macam soal-soal dan pembahasan untuk bisa anda pelajari juga sehingga anda memahami ihwal soal yang ketika ini anda ingin pelajari.
Untuk selengkapnya perihal Soal Luas Bangun Datar tersebut kau bisa simak dibawah ini selengkapnya untuk anda semua, biar bisa menjadi faedah untuk pelajaraan anda dikala ini.
Luas gabungan berdiri datar mampu dicari dengan membagi berdiri datar tersebut menjadi beberapa bangkit yang menyusun adonan bangkit datar tersebut. Untuk mampu mengerjakan soal luas adonan bangun datar diperlukan kesanggupan untuk mencari ukuran dari salah satu sisi dari bangun datar tersebut. Biasanya sisi tersebut ukuranya tidak dituliskan eksklusif, namun mesti dicari dengan memakai ukuran yang telah ada. Dalam melaksanakan soal gabungan berdiri datar ini dibutuhkan ketelitian dalam memilih ukuran sisi dari bangun datar tersebut. Berikut ini beberapa contoh soal luas adonan bangun datar.
Contoh 1
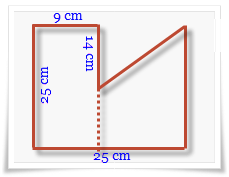
1. Perhatikan Gambar di samping !
Luas Gabungan berdiri datar di samping ialah. ….cm²
- a. 513
- b. 625
- c. 801
- d. 863
Luas bangkit di samping mampu dicari dengan cara membagi kedua bangun tersebut menjadi 2 buah bangun ialah bangun persegi panjang dan trapesium
a. Luas persegi panjang
Luas = p x l = 25 x 9
= 225²
b. Luas Trapesium
Tingi trapesium = 25 cm – 9 cm = 16 cm
Panjang a = 25 cm -14cm = 11 cm
Luas = (a+b) x t/2
= (11 + 25 ) x 16/2
= 36 x 16/2
= 576/2
= 288²
Luas gabungan = 225 + 288 = 513²
Atau bisa juga menggunakan Luas persegi – Luas segitiga
a. Luas persegi = s x s = 25 x 25 = 625 cm²
b. Luas segitiga, tinggi segitiga = 25 cm -9 cm = 16 cm
Luas segitiga= ½ x a x t
= ½ x 14 x 16
= ½ x 224²
= 112
Luas Gabungan = 625 – 112
= 513 cm²
Contoh 2
2. Perhatikan gambar di samping !
Luas bangkit di samping yaitu. ….cm²
- a. 886
- b. 882
- c. 868
- d. 828
Luas adonan bangun di samping dapat dicari dengan memakai Luas belah ketupat dan Luas trapesium
a. Luas Belah ketupat d1 = 2 x 18 cm, d2 2 x 14 cm
Luas belah ketupat = ½ x d1 x d2
= ½ x 36 x 28
= ½ x 1.008
= 504 cm²
b. Luas trapesium = (a + b) x t/2
=(14 +28) x 18/2
= 42 x 18/2
= 756/2
= 378²
Luas adonan = 504 cm² + 378 cm²
= 882 cm²
Contoh 3
3. Perhatikan gambar di samping !
Luas bangun di samping adalah. ….dm²
- a. 20
- b. 25,5
- c, 30
- d. 32
Luas gabungan bangkit di samping mampu dicari memakai luas persegi panjang dan luas segitiga
a. Luas persegi panjang = px l = 8 dm x 3 dm = 24 dm²
b. Luas segitiga = ½ x a x t
= ½ x 4 dm x 4 dm
=½ x 16 dm
= 8 dm²
Luas campuran = 24 dm² + 8 dm² = 32 dm²
Contoh 4
4. Perhatikan gambar di samping !
Luas kawasan yang diarsir pada gambar di
samping yakni. ….cm²
- a. 353,5
- b. 350
- c. 250
- d. 238
Luas daerah yang diarsir dapat dicari memakai Luas trapesium – luas bundar
a. Luas trapesium = (a + b) x t/2
= (21 + 35) x 14
= 56 x 14
= 784/2 = 392 cm²
Luas lingkaran = πr²
= 22/7 x 3,5²
= 38,5 cm²
Luas gabungan = 392 cm² – 38,5 cm²
= 353,5 cm²
Contoh 5
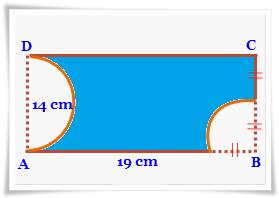
5. Perhatikan gambar di samping !
Luas bangkit datar di samping ialah. …cm²
- a. 245,8
- b. 248,5
- c. 254,8
- d. 258,4
Luas bangun di samping mampu dicari dengan menggunakan luas persegi panjang – luas 3/4 bundar.
a. Luas persegi panjang , panjang = 19 + 7 cm = 26
Luas persegi panjang = p x l = 14 x 26
= 364 cm²
b. Luas 3/4 bulat = 3/4 πr²)
=3/4 x 22/7 x 7²
= 3/4 x 154
= 115, 5 cm²
Luas gabungan = 364 cm² – 115,5 cm²
= 248,5 cm²
sumber: mastugino.blogspot.co.id